A super important notion in linear algebra is that of duality. Put simply, duality is the following fact:
there is an isomorphism between vectors and linear functionals
The lay-man’s explanation of this is “the dual of a column vector is a row vector, sometimes also called the transpose”. I don’t think this really does the idea justice though.
The way I like to think about it is like this. Let’s say that we have a vector space \(V\), with some basis \(e_1,\ldots, e_n\). Then, the dual space \(V^*\) is the set of linear-functionals on \(V\). \(V^{*}\) has a basis \(\hat{e_1}, \ldots, \hat{e_n}\) which are the linear functionals that act as follows on vectors \(v=c_1 e_1 + c_2 e_2 + \cdots\): \[\hat{e_i}(v) = c_i.\]
It’s kinda interesting. Think about it a bit.
Let’s see this in action, to solve the following problem:
Theorem. \(Im A = Im AA^T\)
But actually this isn’t the real theorem. The real theorem is:
Theorem. Let \(A: \mathbb{R}^n \to \mathbb{R}^m\), and \(A^T : \mathbb{R}^m \to \mathbb{R}^n\). Then
\[\ker A^{T} \oplus Im A \cong \mathbb{R}^m\] \[\ker A \oplus Im A^T \cong \mathbb{R}^n.\]
and in-fact, \(\ker A^T\) is the orthogonal complement of \(Im A\); similarly \(\ker A\) is the orthogonal complement of \(Im A^T\).
This theorem immediately implies the other theorem via the following picture 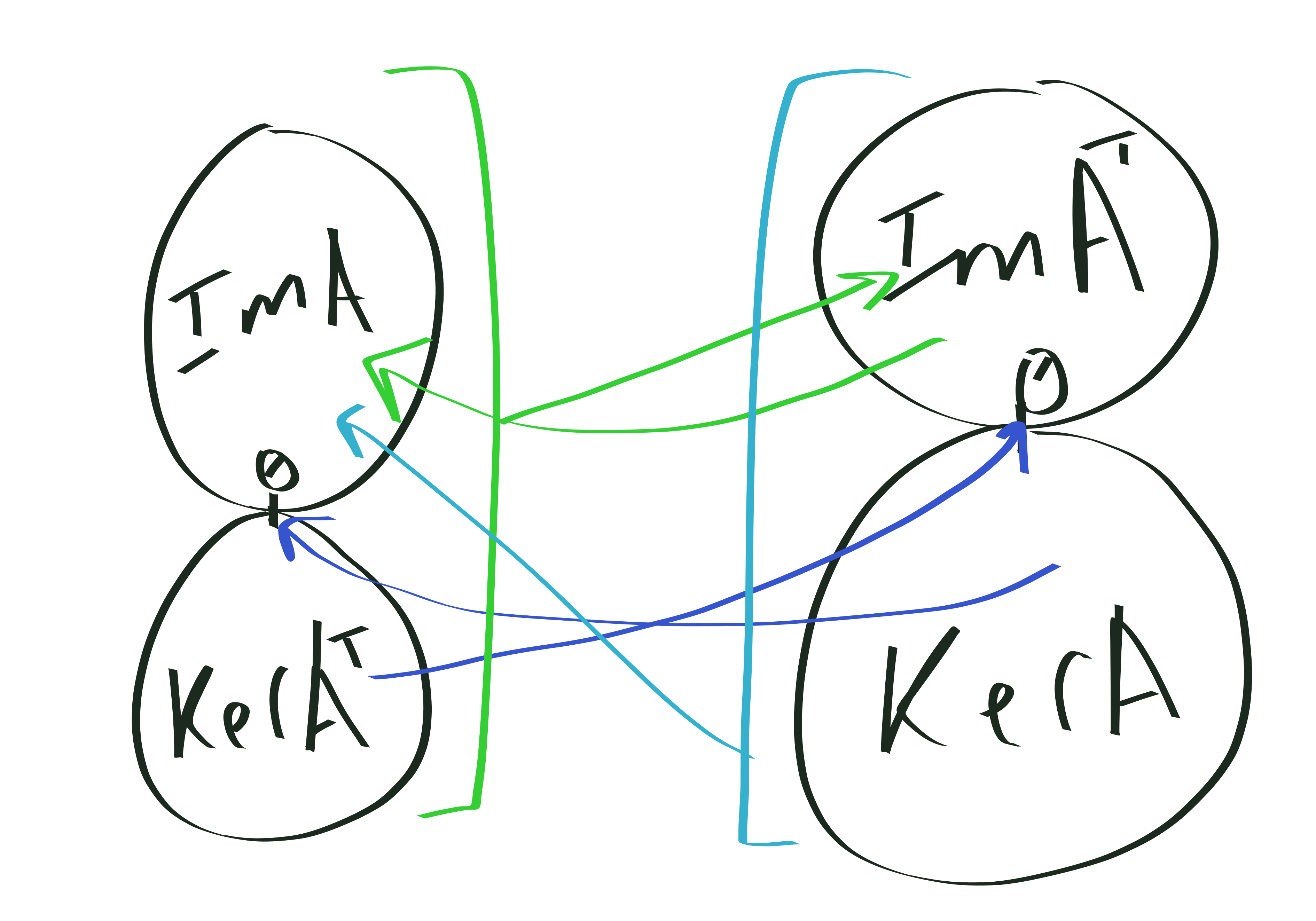
Proof. Say \(A^T y = 0\). Then \(y^T A = 0\), so \(y^T A x = 0\) for all \(x\), i.e. \(y \perp Ax\).