We aim to bound \[\sum_{i\leq \epsilon n} \binom{n}{i}\]
The answer, roughly speaking, should be \(c(\epsilon)^n\) for some \(1 \leq c(\epsilon) \leq 2\).
We can think of this probabilistically as being related to the following problem: Let \(X_1,\ldots, X_n\) be independent random variables with probabilty \(1/2\) of occuring. These random variables represent taking a subset of \([n]\). Then we are concerned with \[\Pr[\sum X_i \leq \epsilon n].\]
In particular, \[\Pr[\sum X_i \leq \epsilon n] = 2^{-n} \sum_{i\leq \epsilon n}\binom{n}{i}.\]
Applying one form of the Chernoff bound listed on wikipedia we can bound our sum by
\[\Pr[\sum X_i \leq \epsilon n] \leq \left(\frac{2}{\sqrt{e}}\left(\frac{e}{2\epsilon}\right)^\epsilon\right)^n.\]
Remark. This is basically tight for \(\epsilon \approx 1/2\), and pretty decent for e.g. \(\epsilon\in (.1,.5)\).
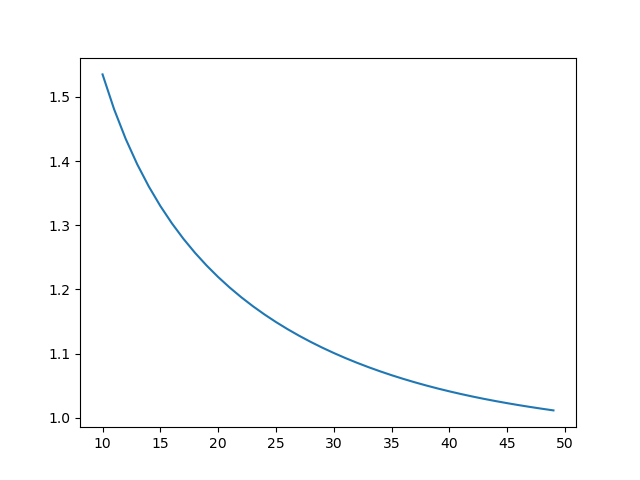
import matplotlib.pyplot as plt
from math import comb, sqrt, log2, e
n = 100
idxs = list(range(n//10,n//2))
actual = [1 for k in range(n)]
log_estimate = []
for k in range(1,n):
actual[k] = actual[k-1] + comb(n, k)
eps = k/n
log_estimate.append( log2(2/sqrt(e)) + eps*log2(e/(2*eps)) )
log_actual = [log2(a)/n for a in actual]
ratio = [log_estimate[i]/log_actual[i] for i in idxs]
plt.plot(idxs, ratio)
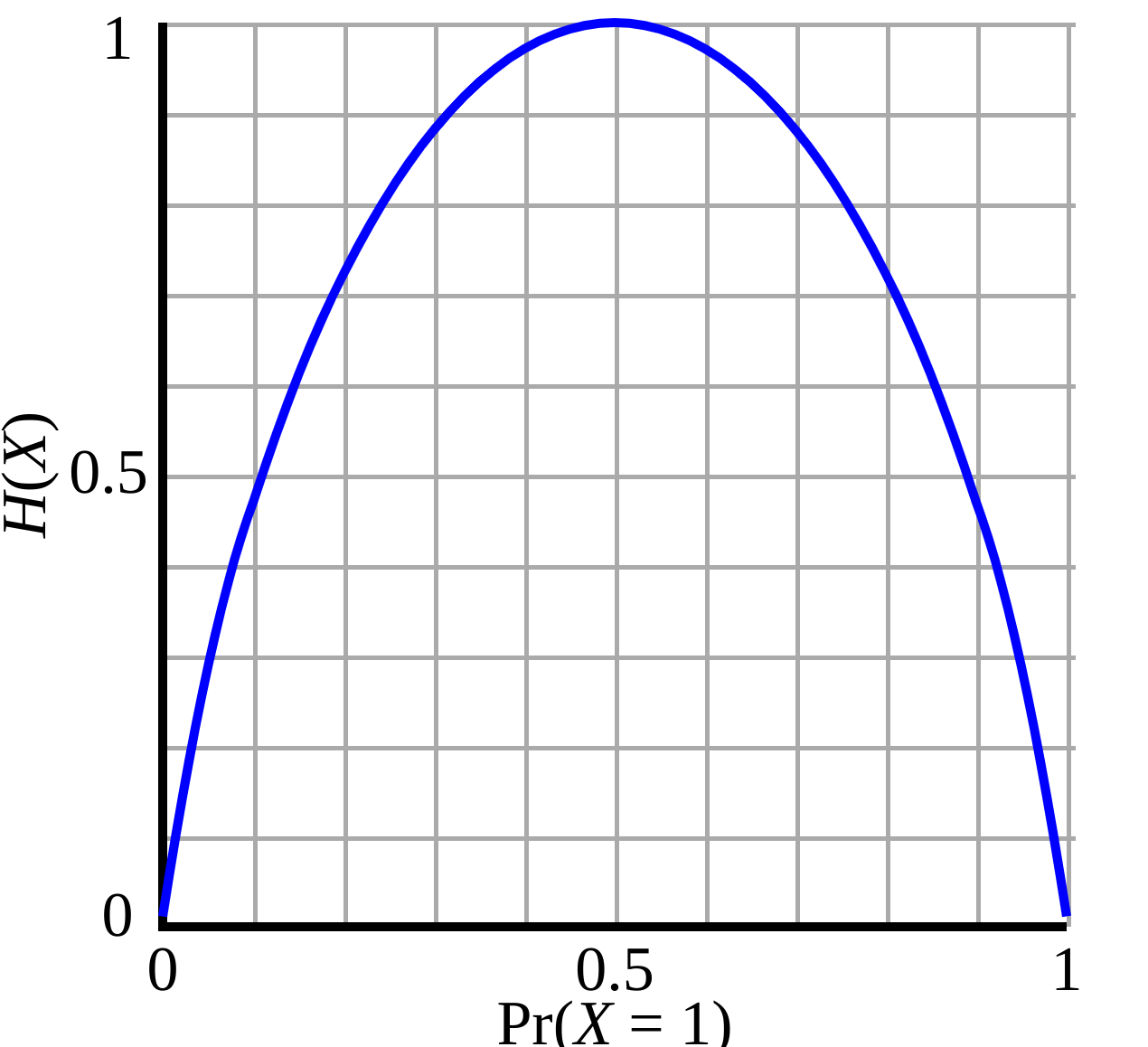
plt.show()UPDATE OK, apparently the answer can be expressed in terms of \(H\), the binary entropy function: \[\Pr[\sum X_i \leq \epsilon n] \approx 2^{H(\epsilon)n}.\]