Imagine you had \(p\) elevators, which took time \(1\) to move between floors and time \(W\) to stop at a floor, and had capacity \(L\). People arrive at times \(t_i\) and you want to optimize some objective function.
To start we take the goal of minimizing the total time that is required to transport all of the people assuming that they all arrive at time \(0\).
Proposition. For \(p=1,W=0,L=\infty\) there is a simple linear time algorithm to compute an optimal schedule
Proof. The best thing to do is to go up, zig-zagging on some levels, and then at some point just commiting to going to the top of the elevator and then coming back down.
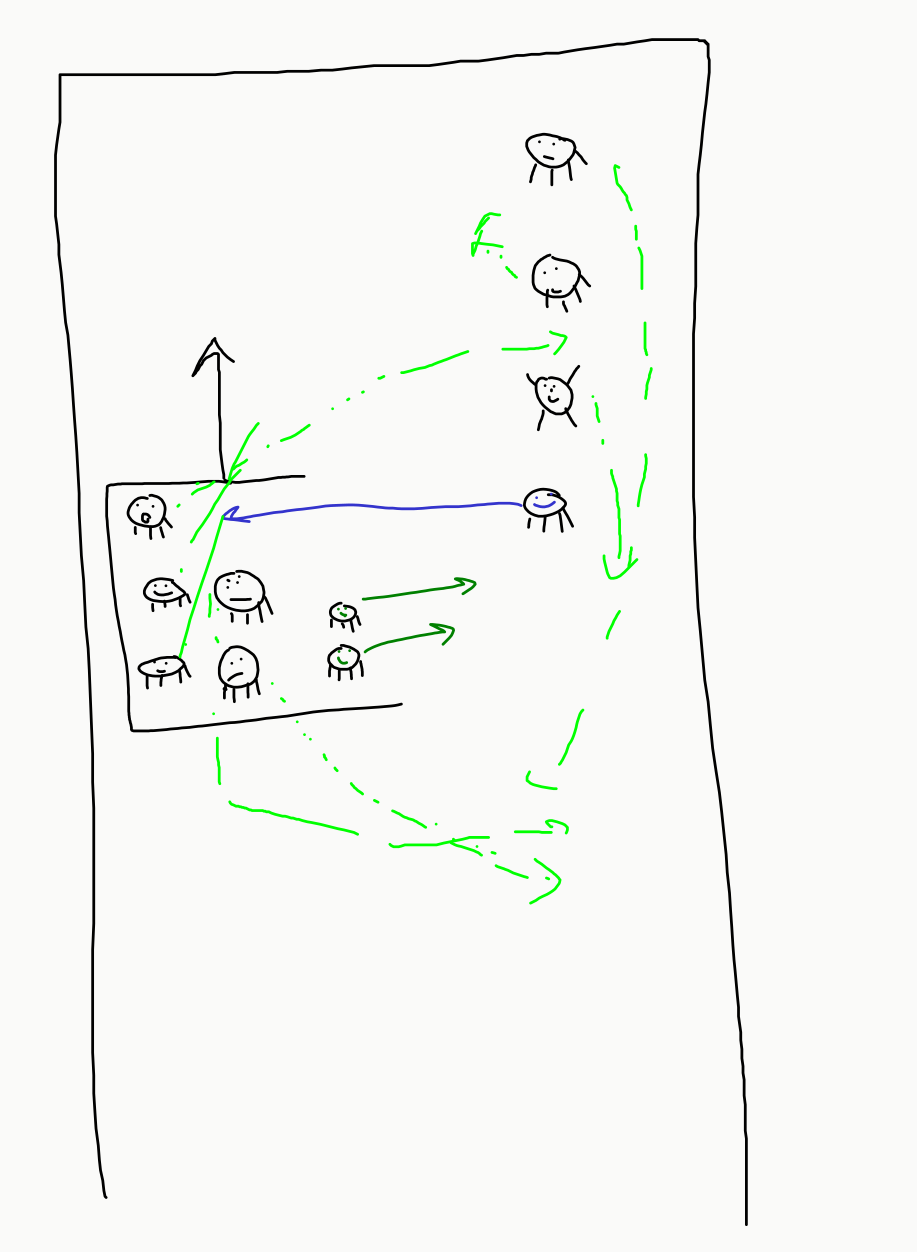
Theorem. For \(p=1,W\gg 1,L=\infty\) the problem reduces to computing “minimum feedback vertex set” i.e. a minimal set of vertices whose removal leaves a cycle-free graph. Unfortunately this problem is NP-hard, even to get a constant approximation to. However, for our application we can still do a \(2\)-approximation to the best elevator schedule by just visiting each node in the SCCs twice. Alteranteively we can get an exact solution in time \(n^2 2^n.\)
Proof. Compute strongly connected components. We will have some set of vertices that we need to visit twice within each connected component. If we leave out these vertices it should be possible to just visit each of the remaining vertices once.
What’s next? I think trying \(\ell_1\)-norm as an objective function, also known as mean response time, would be a next good step. Another good step would be realizing teleportation in the physical world.
update Here is a \(2\)-approx for \(\ell_1\)-norm: Let the number of people on the floors be \(c_1\geq c_2\geq \cdots.\) Strategy: pick up the floor that has the most people on it, then drop that off. repeat! performance: \(\sum c_j 2j\) worst case.
How good is this?
Lower bound for OPT: \(\sum c_j (1+j)\)
So we are definitely \(2\) competitive.