Consider a \(t\)-coloring of \([k]^d\) (i.e. a \(k\times k \times k \cdots\) cube). For instance, if \(k=3,d=2,t=2\) and our colors are “X” and “O” then this corresponds to placing X’s and O’s in a \(3 \times 3\) grid. A “monochromatic combinatorial line” in \([k]^d\) is generated by a string that looks kind of like \(1*4**2*5\). In particular, this string is encoding a size \(k\) subset of \([k]^d\). For instance in tick-tack-toe, \(1*\) would correspond to the set \(\left\{ 11,12,13\right\}\) i.e. a line in the first row of the tick tack toe board. Similarly, \(**\) would correspond to the diagonal \(\left\{ 11,22,33\right\}\).
We all know tick-tack-toe can end in a tie, although I bet I can still beat you more often then not.
However, an interesting question is, if you played really high dimensional tick tack toe would it still be possible to end in a tie? It turns out, the answer is no.
Theorem. For any \(t,k\), there exists \(d\) sufficiently large so that any \(t\)-coloring of \([k]^d\) must contain a monochromatic combinatorial line.
We proceed by induction on \(k\). Assume that we have proved the statement for \(k-1\) and all \(t\). Now we aim to establish it for \(k, t_0\), for some fixed \(t_0.\) We do so by the following lemma:
Lemma. There is a \(d\) such that \([k]^d\) either just has a monochromatic combinatorial line, or it has \(j\) combinatorial lines that are monochromatic besides their endpoints, and these lines all share an endpoint and all have distinct colors.
Proof. We take \(d'\) large enough that the lemma holds for \(j-1\). We take \(d''\) large enough that \(t^{k^{n'}}\)-colorings of \([k-1]^{d''}\) have monochromatic combinatorial lines. We claim that \(d=d'+d''\) is large enough to establish the lemma for \(j\). Here is a proof by picture:
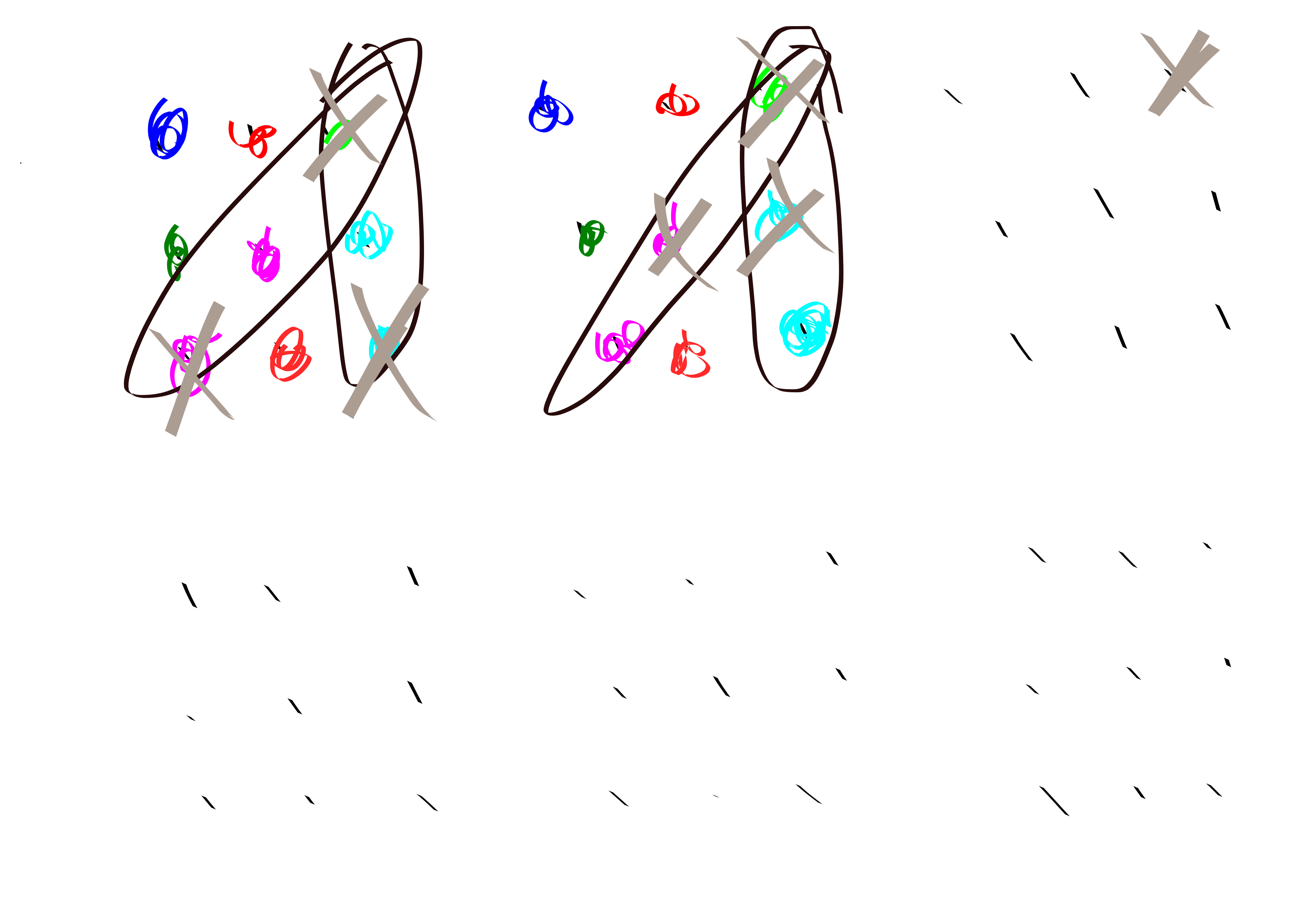
Proof. We use the lemma until we supposedly get \(t_0\) lines each of distinct color with common endpoint. One of them has to have color the same as the endpoint. So we just win.