Theorem. Let \(n = \sum a_i p^i, m = \sum b_i p^i\) be the base \(p\) representations of \(m,n\). Then, \[\binom{n}{m} \equiv \prod \binom{a_i}{b_i}\mod p.\]
Lemma. \[\binom{ap+b}{cp+d} \equiv \binom{a}{c}\binom{b}{d} \mod p\]
Proof. Without loss of generality we take \(a\neq 0\), \(ap+b>cp+d\); otherwise the lemma is trivial.
Think of the \(n\) points as divided into \(a\) groups of size \(p\) with \(b\) left over.
One way of choosing \(cp+d\) points is to saturate \(c\) of the groups and then distribute the \(d\) remaining points among the \(b\) left over points; note that this is only possible if \(d\leq b.\) There are \(\binom{a}{c}\) ways to choose which groups to saturate, and \(\binom{b}{d}\) ways to choose how to fill the left over points.
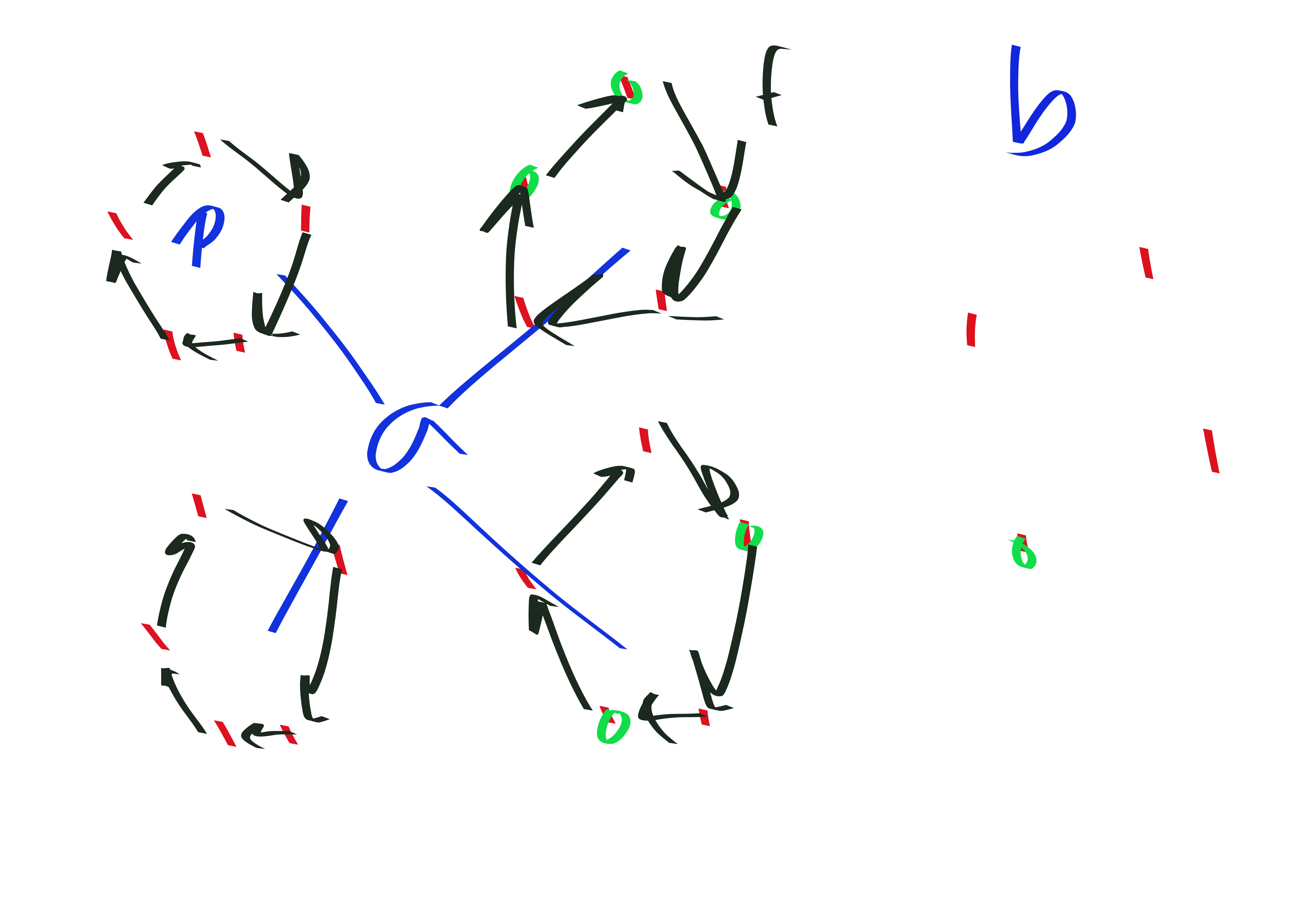
Otherwise, we have an arrangement that partially fills one of the groups. Now consider the map \(f\) which creates a new subset by cycling the elements chosen within each group \(\mod p\). Clearly \(f^p = id\), and \(f\neq id\) because one of the groups was partially filled. Now \(f\) can’t possibly have order less than \(p\), so we have shown that there are \(p\) subsets in the equivalence class generated by the action of \(f\) on the subset. In other words, the number of subsets which partially fill one of the groups is divisible by \(p\).
Hence, only the earlier computed term $ $contributes to the binomial coefficient \(\mod p.\)