Shatar is thinking of selling a pizza and Blobby is thinking of buying a pizza. Shatar and Blobby’s valuation of the pizza will both be independently uniformly random on \([0,1]\) tomorrow. This fact is common knowledge and everyone knows it is common knolwedge, and everyone knows everyone knows it is common knolwedge etc.

Shatar and Blobby will play the following game tomorrow:

• Shatar and Blobby discover their own valuations \(s\gets [0,1], b\gets [0,1]\)
• Shatar and Blobby report some values \(\hat{s}, \hat{b}\).
• The trade goes through iff \(\hat{b} > \hat{s}\)
• If the trade goes through then it goes through at price \(P = \frac{\hat{b}+\hat{s}}{2}\)
• If the trade goes through Shatar gets utility \(P-s\) and Blobby gets utility \(b-S\)
• If the trade doesn’t go through Shatar and Blobby both get \(0\) utility.

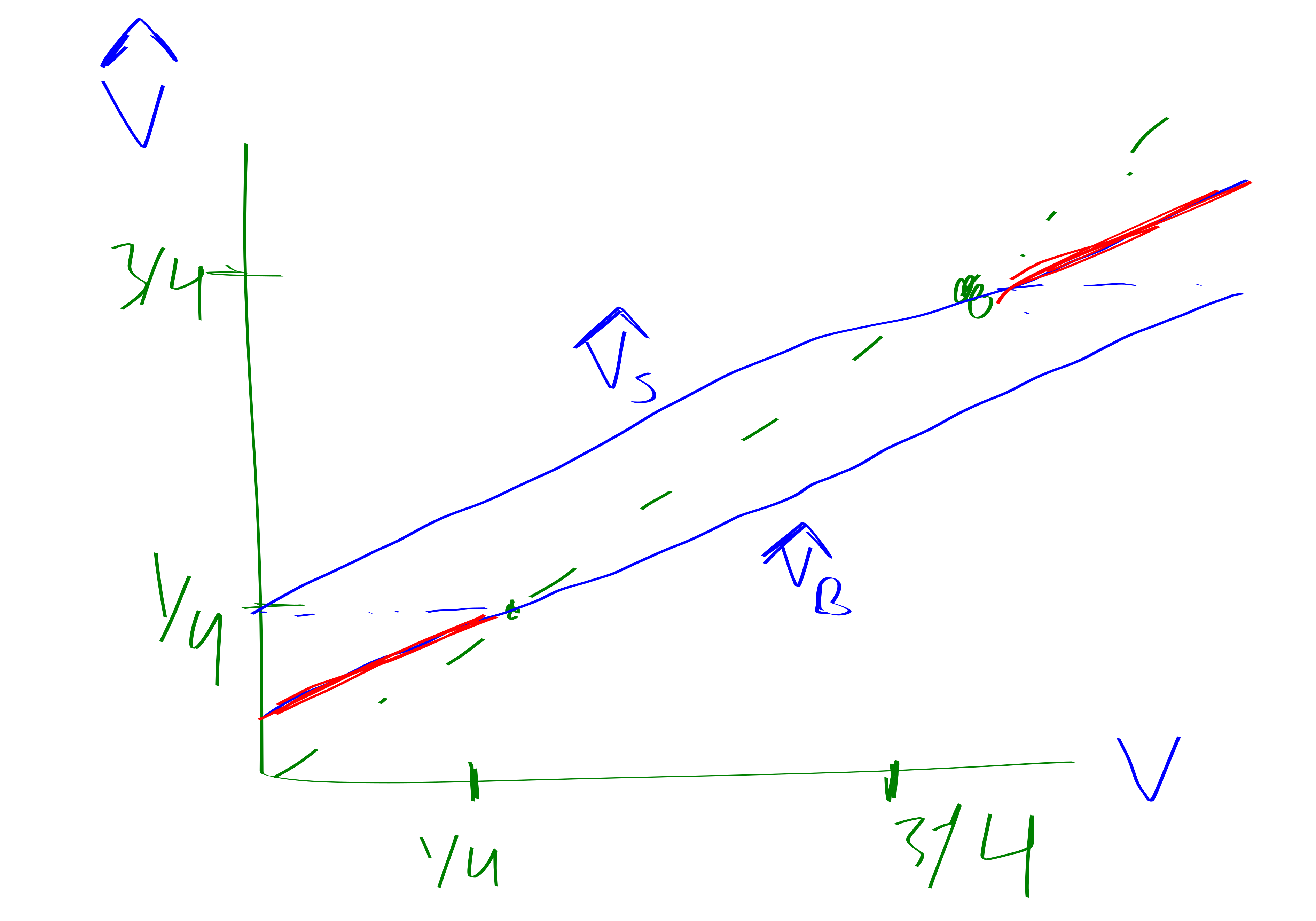
It turns out the Nash equilibrium is as follows:

• \(\hat{s} = \frac{2}{3}s + \frac{1}{4}\)
• \(\hat{b} = \frac{2}{3}b + \frac{1}{12}\)

This is kind of weird! Luckily the trade never goes through if \(b<\frac{1}{4}\) or if \(s>\frac{3}{4}\) which makes it make a bit more sense.

I find the fact that the equilibria is linear lies to be very interesting.

I guess the moral of the story is sometimes you should lie.