introduction
An \(\exists \mathbb{R}\) formula (ETR) is defined as follows: You form a sentance \(\Phi\) using variables \(X_1,\ldots,X_n\) and the symbols \(\lor, \land, \neg, 0, 1, +, -, \cdot, (,),=, <, \le\). The formula is then \[ \exists X_1,X_2,\ldots, X_n\in \mathbb{R}\mid \Phi(X_1,\ldots, X_n). \] The language \(\exists \mathbb{R}\) is the set of all true \(\exists \mathbb{R}\) formulas.
Conway proved that \(\exists \mathbb{R}\subseteq \mathsf{PSPACE}\). It is clear that \(\exists \mathbb{R}\supseteq \mathsf{NP}\).
Note that we can encode constants other than \(0,1\) by adding \(1\) to itself many times and then dividing. However, the length in bits of the numerator and denominator of a rational fraction will influence the formula length.
A simple example of an \(\exists \mathbb{R}\) formula is a formula for checking if an intersection of half-planes with rational slopes is empty. To build such a formula we first note that the determinant can be used to check if one vector is to the left or to the right of another vector. For rational numbers \(a_1,b_1,a_2,b_2\) we define the proposition \(\Phi_{L((a_1,b_1),(a_2,b_2))}(x,y)\) for checking if point \(x,y\) lies above the line that passes through \((a_1,b_1), (a_2,b_2)\) as follows: \[ (a_2-a_1)(y-b_1)-(x-a_1)(b_2-b_1) \ge 0. \] Now, given several half-planes we can write a formula of the form \[ \exists x,y \mid \Phi_{L((a_1,b_1),(a_2,b_2))} \land \Phi_{L((a_3,b_3),(a_4,b_4))} \land \Phi_{L((a_5,b_5),(a_6,b_6))} \] and this formula is satisfied by some \(x,y\in \mathbb{R}\) if and only if the intersection of half-planes described by the formula is non-empty.
It is also worth noting that you can force variables to take irrational values (although the values will always be algebraic). For instance, the formula: \[ \exists x \mid x\cdot x = 2, \] forces \(x=\sqrt{2}\).
Containment in \(\exists \mathbb{R}\)
Theorem. Let \(P,g\) be an instance of the art gallery problem, where \(P\) is a polygon with \(n\) vertiecs, each of which has rational coordinates represented by at most \(B\) bits. There is a polynomial time algorithm that turns \(P,g\) into an \(\exists \mathbb{R}\) formula \(\Phi\) such that the \(\exists \mathbb{R}\) formula has length \(O(n^{14}B^2)\) and such that the \(\Phi\) is satisfiable if and only if \(P\) can be guarded by \(g\) guards.
Proof. First we show how to turn an art gallery problem into a simple formula which is not quite in the \(\exists \mathbb{R}\) class of formulas, but is quite close. Specifically, the problem will be that it has a \(\forall\) quantifier. The formula is as follows: \[ \Psi := \exists x_1,y_1,\ldots, x_k, y_k \forall p_x,p_y \mid \text{INSIDE-POLYGON}(p_x,p_y)\implies \lor_{i=1}^{k} \text{SEES}(x_i,y_i,p_x,p_y).\] Now we expand out the INSIDE-POLYGON and SEES sub-formulas. INSIDE-POLYGON can be implemented by triangulating the polygon and doing an \(\lor\) of checks for if the point \(p_x,p_y\) is in each of the triangles. To check containment in a triangle we can exactly use the formula described earlier in this note for checking intersection of half planes. We simply orient the edges of the trianlge counter-clockwise and then check if the point is to the left of each of these edges. The INSIDE-POLYGON predicate has length \(O(nB)\).
For the SEES predicate we insert, for every pair of consecutive edges, a predicate that checks if \(e_1,e_2\) blocks the line of sight between \(p_x,p_y\) and \(x_i,y_i\); this can be done with a constant number of determinants.
To convert the formula \(\Psi\) into an ETR formula we create a witness set: a small subset of points such that if these points are guarded then it guarantees that the entire polygon is guarded.
Roughly speaking the witness set is constructed as follows: Let \(L\) denote the set of lines containing either an edge of \(P\) or a guard \(g\) and a corner \(v\) of the polygon (modulo an issue that this is not well defined if a guard is placed on a corner). The lines divide \(\mathbb{R}^2\) into regions (faces of the arrangement). The set of regions satisfies:
- each region is an open convex polygon
- each region is either fully inside the polygon or fully outside
- the closure of the union of the regions inside the polygon gives the entire polygon including the boundary
- For each region \(R\) and each guard \(g\) we have that \(g\) either sees all of \(R\) or none of \(R\).
So, what we will do is, for each region \(R\) contained in the polygon we choose a point in the interior of \(R\), namely the centriod of \(3\) distinct points. Then we add a check for if there is a guard that can see this internal point. The entire polygon is guarded if and only if each of these internal points is seen by some guard.
The way they handle the possibly degenerate lines and the possibility of parallel lines is kind of as follows:
- for each pair of (potentially degenerate) lines they have a formula that asserts that either (a) one of the lines is degenerate, or (b) the lines are parallel, or (c) some variable gets assigned to have value equal to this intersection point.
- then they a condition that says, for each triple of points, if those three points are all defined, then force some variable to be made equal to the centroid and if that centroid is inside the polygon, then force some guard to see it.
\(\exists \mathbb{R}\) hardness
The first hint that the art gallery problem might be harder than NP-hard is that there are polygons where it is necessary to place the guards at irrational points.
[TODO: draw example]
The hardness proof is based on the following simpler but equivalent variant of ETR, which they call ETRINV:Theorem. The variables \(x_1,x_2,\ldots, x_n\) all must be within \([1/2,2]\). The allowed constraints are of the following form:
- \(x_i = 1\)
- \(x_i + x_j = x_k\)
- \(x_i\cdot x_j = 1\)
Deciding satisfiability of ETRINV is just as hard as deciding satisfiability of ETR.
The proof of this theorem is some rather involved algebra.
Now we outline the components of their proof. They will have variable gadgets at the bottom and clause gadgets on the sides.
The variable gadgets look like this:
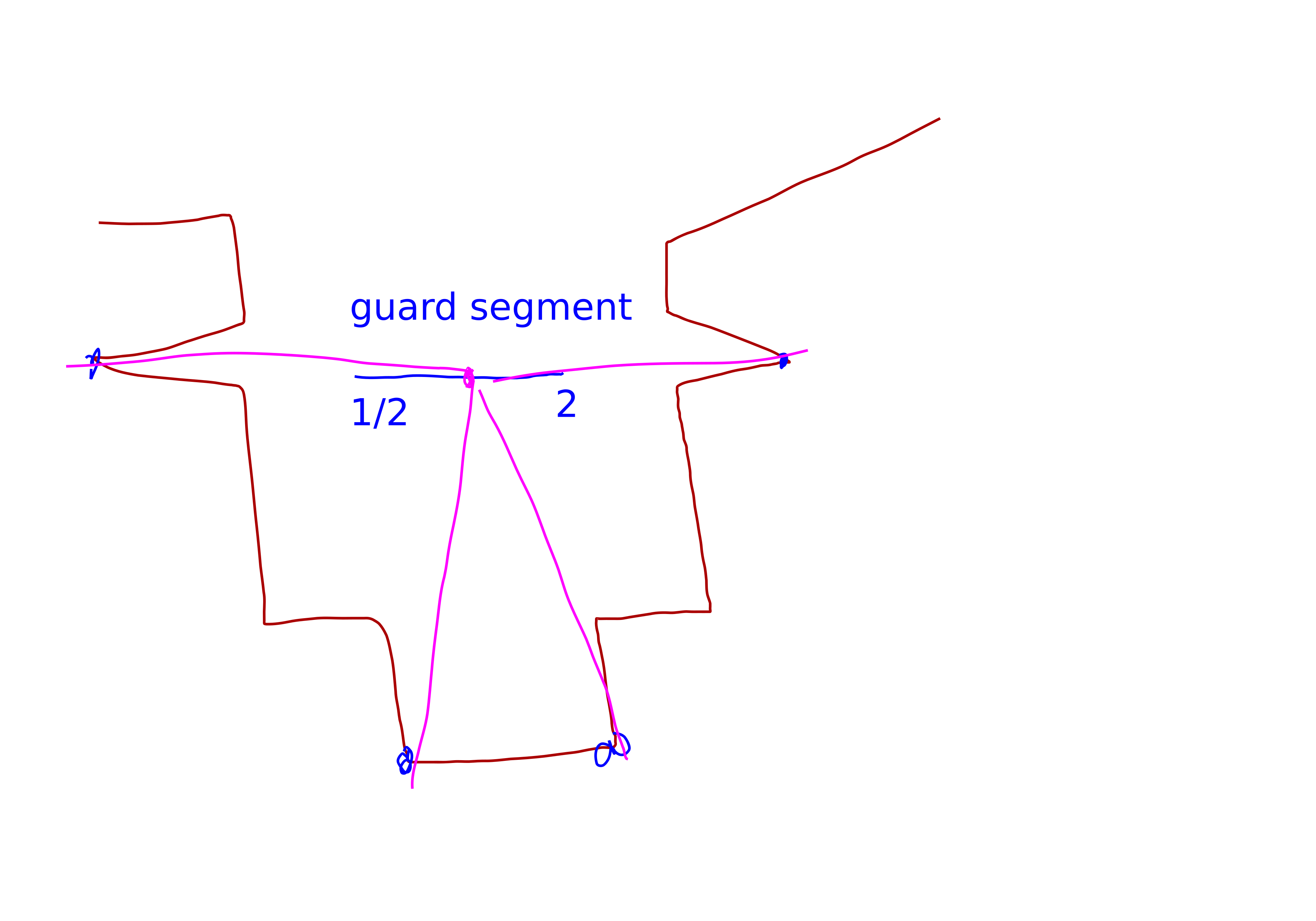
The idea is, in order for a guard to be able to see all of the 4 corners it needs to be somewhere on the “guard segment”. The location on the guard segment will encode the variable’s value.
They also need a variation of this with some extra pockets to enforce \(x_i = 1\) constraints.
Next they need a copy gadget.
Then they need an addition gadget.
Finally they need an \(x=1/y\) gadget.
These gadgets are cool but very tricky to construct and required some computer search.
open questions
- Is guarding the boundary \(\exists \mathbb{R}\) complete? Actually this was recently resolved by Jack Stade.
- interesting note: you can guard the boundary without guarding the interior.
line guard problem
In the line guard problem you are given a polygon and number \(k\). The question is, can you draw \(k\) line segments inside the polygon such that if you had guards patrolling those line segments then every point in the polygon would be visible at some point in time? This is called weak visibility.
Now we try to adapt the \(\exists \mathbb{R}\) containment proof from above to the line guard problem.
Theorem. (hopefully will prove this???)
Deciding whether an art gallery polygon \(P\) is weakly-line-guardable by \(k\) guards is solvable in \(\exists \mathbb{R}\).
Proof.
First we write a formula with (illegal) \(\forall\) quantifiers. I’m cautiously optimistic that the same “witness points” from above can help us just \(\forall\) over a finite set of witness points (aka, finite \(\land\), which is legal) rather than the continuum of points in the interior of the polygon. Anyways the formula looks like this:
\[ \exists (a_1,b_1,c_1,d_1),\ldots,(a_k,b_k,c_k,d_k) \mid \forall x,y: \exists t_1,\ldots,t_k\] such that \[ \text{INSIDE POLYGON}(x,y) \implies \bigwedge_i t_i\in [0,1] \bigvee_{i} (a_i,b_i)t+(c_i,d_i)(1-t) \text{ SEES } (x,y). \]
Yeah, so tldr is I think the witnes set thing from earlier is also going to just win this one.
Like, here’s the idea. TODO: NO THIS IS NOT RIGHT Imagine we had a set \(W\) of polynomial size with the following property: \[ \forall (x,y)\in W \exists (x',y') \in S \mid (x',y') \text{ SEES } (x,y) \implies \forall (x,y)\in P \exists (x',y') \in S \mid (x',y') \text{ SEES } (x,y).\]
Let \(W = (x_1,y_1),(x_2,y_2),\ldots.\) Then, we’d be pretty happy with the following formula: \[ \exists (a_i,b_i,c_i,d_i)_{i\in [k]} (t_{ij})_{i\in [k], j\in [|W|]}\] such that \[\bigwedge_{ij} t_{ij}\in[0,1] \bigwedge_{j\in [|W|]} \bigvee_{i} (a_i,b_i)t_{ij}+(c_i,d_i)(1-t_{ij}) \text{ SEES } (x_j,y_j). \]
Anyways, I think this is basically what their witness set is.
ok actually I need to be more careful, because the definition of the witness set thing depends on the coordinates of the guards. so yeah let’s do take 2.
nope this is just not going to work.