Simple Kernels
Vertex cover is covered (hahahaha) in a different blog post.
FAST: Feedback arc set in Tournaments
(find a set of edges “hitting” all the cycles)
Lemma. A minimal (in the sense that if you delete any edge from the set the property fails; not necessarily minimum) set of edges in the whose reversal in the tournament results in a DAG is also a minimal (in the same sense as above) feedback arc set.
Proof.
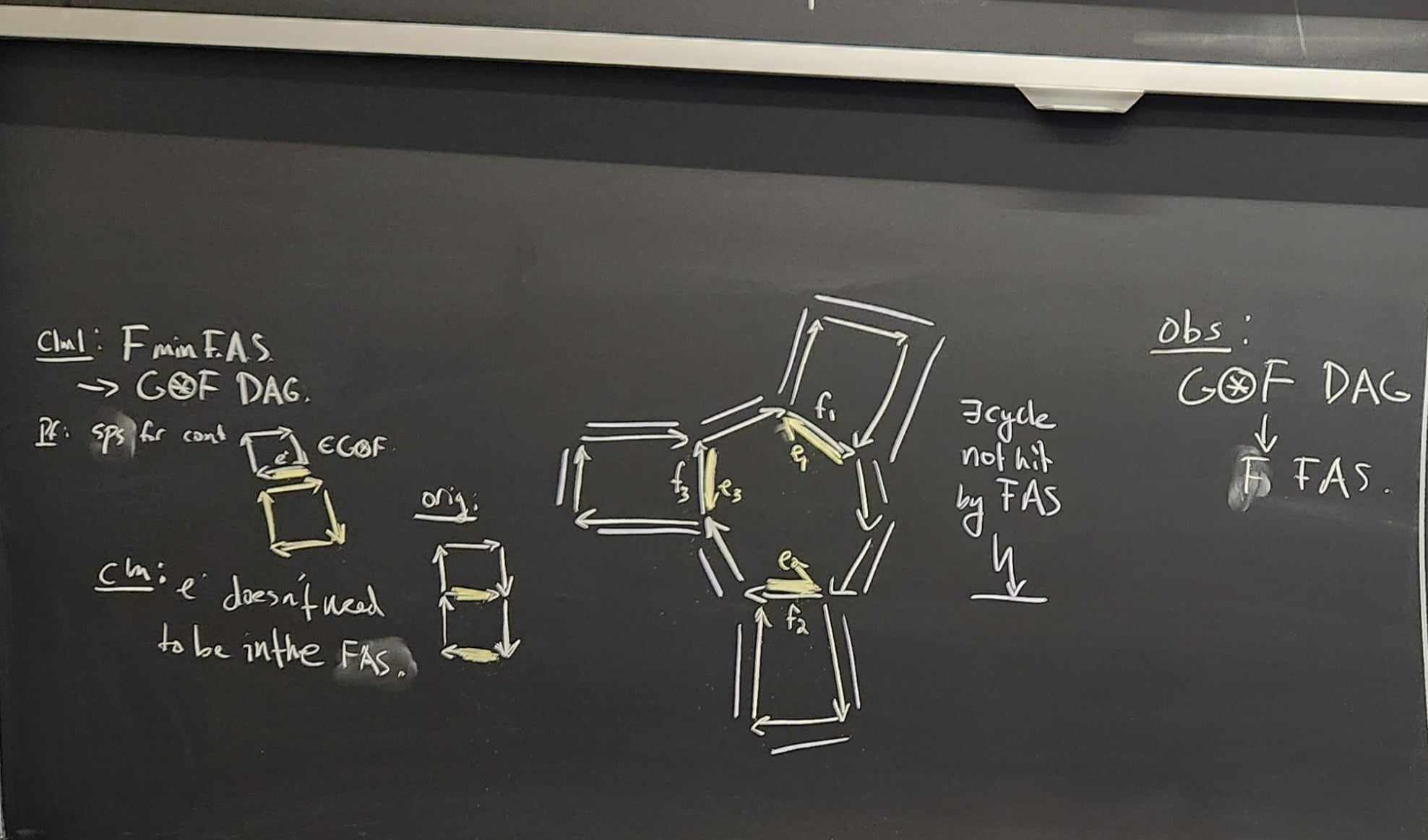
Theorem. nice kernel for FAST
Proof.
- must take edges involved in more than \(k+1\) triangles
- is safe to delete vertices not involved in any triangle
- at this point I think you get a bound of like \(O(k^{2})\) on number of edges in a YES instance based on the two above reductions.
ECC: edge clique cover. cover edges by cliques.
Theorem. \(2^{k}\) sized kernel
Proof.
it is safe to delete connected components which are already cliques (and decrease \(k\) by one here).
it is safe to merge “true twins”: vertices with identical (closed) neighborhoods.
At this point we claim that in any YES instance there are at most \(2^{k}\) vertices left. Assume for contradiction that we have a YES instance, i.e., there are cliques \(C_1,C_2,\ldots, C_k\) covering all the edges, but we have more than \(2^{k}\) vertices.
Then associate a \(k\)-bit vector with each vertex indicating which of the \(C_i\) clique’s its part of.
By pidgeon two vertices share an indicator vector. That means they are true twins, a contradiction.
LP-based kernels
A lot of NP-hard problems are easily phrased as ILPs. ILP is hard. But often we can get a lot of info about what the ILP solution should look like by relaxing to an LP.
Vertex cover LP relaxation:
\[\forall uv\in E, x_u + x_v \ge 1\] \[\forall v\in V, x_v \in [0,1]\] \[\min \sum_{v\in V} x_v.\] We can think of this as a “fractional vertex cover”.
Lemma. Take an LP solution. Let \(V_0\) be vertices in the LP solution with \(x_v< 1/2\) Let \(V_{1/2}\) be vertices with \(x_v=1/2\) and finally let \(V_1\) be vertices with \(x_v>1/2\).
Then, it turns out that there is a minimal vertex cover \(S\) satisfying:
\[V_1 \subseteq S \subseteq V_1\sqcup V_{1/2}.\]
Proof.
Take any minimum vertex cover \(S^*\). Form \(S\) by taking \(S^{*}\) and removing the \(V_0\)’s and adding any missing \(V_1\)’s.
Claim: \(S\) is also a minimum VC. proof: by contradiction. Specifically, assume \(S\) is a worse VC. Turns out we can use this to show that the LP solution that generated \(V_0,V_{1/2},V_1\) was actually suboptimal.
Theorem. Vertex Cover kernel
Proof. Run LP (actually you don’t need to, you can do some kinda flow thing instead of actually running LP; but same effect).
Toss \(V_0\). Take \(V_1\). Size of \(V_{1/2}\) can’t be too large or we auto reject.
Crown Lemma
We say a matching “saturates” a set if there is an edge incident to all the vertices in that set.
KONIG - bip. graph: max matching = min vertex cover
HALL: bip graph \(G\) with vertex bipartition \((V_1,V_2)\). - \(G\) has a matching saturating \(V_1\) iff for all \(X\subset V_1\) we have \(|N(X)|\ge |X|\).
Lemma. We can use flow or whatever to find max-matching / min-vertex cover in \(O(m\sqrt{n})\) time.
If the max-matching doesn’t saturate \(V_1\), we can find a witness \(X\subseteq V_1\) for which \(|N(X)|< |X|.\)
Definition. Crown:
CHR
C is an indep set. And non-empty there is a C,H matching saturating H. There are no edges between C,R.
Theorem. there is a poly time algo that, on any graph with at least \(3k+1\) vertices either
- outputs a matching of size \(k+1\)
- finds a crown decomposition
Theorem. we can use crown lemma to make a kernel for VC.
Proof. Run crow decomp algo. If you find a matching of size \(k+1\) output NO. Else, you can take the “head” in the crown decomp, and ditch the crown. This allows us to decrease the problem size as long as the problem size is at least \(3k+1\). Hence \(O(k)\) vertex kernel.
Theorem. MAX SAT has a kernel with \(O(k)\) vars \(O(k)\) clauses.
Proof.
Expansion lemma
Now we do a more powerful version of the crown lemma.
Definition. A \(q\)-expansion of \(A\) into \(B\) is each vertex in \(A\) has exactly \(q\) neighbors in \(B\) and these neighbors are disjoint, i.e., \(q|A|\) of the vertices in \(B\) are hit.
You can also think of this as a collection of \(q\) edge-disjoint matchings, each saturating \(A\).
Lemma. Let \(G\) be a bip graph with bipartition \((A,B)\). There is a \(q\)-expansion from \(A\) into \(B\) iff \(|N(X)|\ge q|X|\) for all \(X\subseteq A\). Furthermore, if there is no such \(q\)-expansion we can find a witness in poly time.
Proof.
Replace \(A\) with \(q\) copies of \(A\). Run Hall’s theorem on the new graph. Matchings in this new graph correspond to \(q\)-expansions in the original graph.
Lemma. EXPANSION LEMMA
Suppose we have a bip graph on vtxs \(A,B\) with \(|B|\ge q|A|\) and that there are no isolated vtxs in B.
Then there are \(X\subseteq A, Y \subseteq B\) such that \(q\)-expansion of \(X\) into \(Y\). No vertex in \(Y\) has a neighbor outside of \(X\), i.e., \(N(Y)\subseteq X\).
Remark. \(X, Y, V\setminus (X\cup Y)\) is a crown decomp but with even more properties: not only is every vertex of \(X\) matched into \(Y\) but there is a \(q\)-expansion of \(X\) into \(Y\).
Sun-flower
Definition. SUNFLOWER:
\(k\) petals, core \(Y\): sets \(S_1,S_2,\ldots, S_k\) such that \(S_i \cap S_j = Y\) for all \(i\neq j\) and the “petals” \(S_i \setminus Y\) are all required to be non-empty.
The core can be empty though.
Theorem. Family of sets over a universe. Each set has \(d\) elements. If you have more than \(d!(k-1)^{d}\) such sets then the family contains a sunflower with \(k\) petals. And we can compute it in poly time in terms of the numebr of sets, universe size and \(k\).
Proof. induction
some exercises
Proposition. 2.4 “In the Point Line Cover problem, we are given a set of n points in the plane and an integer k, and the goal is to check if there exists a set of k lines on the plane that contain all the input points. Show a kernel for this problem with \(O(k^{2})\) points.”
Proof. If any line has more than \(k\) points on it, you better take that line. First run this reduction. Now wlog each line has at most \(k\) points on it. Now, if there are more than \(k^{2}\) points output REJECT. Else, we have our desired kernel.
Proposition. “2.7. In the Minimum Maximal Matching problem, we are given an undirected graph G and a positive integer k, and the objective is to decide whether there exists a maximal matching in G on at most k edges. Obtain a polynomial kernel for the problem (parameterized by k).”
Proof.
observation 1: If \(G\) has a \(4k\) vertex matching then it certainly can’t have a maximal matching of size at most \(k\).
Call a vertex “high degree” if its degree is more than \(4k\). Clearly we must take any edge that has two high-degree endpoints.
So, the set of high-degree vertices will form an independent set after we apply the first reduction.
So the story is, we are going to eat up to \(k\) edges. And in order for this to be a maximal matching we need it to be the case that for every edge \(e\in E(G)\) we ate an edge that shares an endpoint with \(e\).
We say that an edge \(e\) is “neutralized” if we take an edge that shares an endpoint with \(e\). Consider an LL edge. Observe that each edge we eat neutralizes at most \(O(k)\) LL edges. Hence, if there are more than \(\Omega(k^{2})\) such edges then we can output REJECT: there is no way we are going to neutralize all the edges.
Otherwise, we have an instance with at most \(k^{2}\) LL edges. The instance technically might still have a lot of vertices though. However we can clean this up. There are at most \(O(k)\) H vertices, or else we can’t hope to cover all of the H vertices.
The final thing we need to clean up is, there might be a ton of L vertices which are just connected to H vertices.
But this is kind of silly. Call an L vertex silly if it only has neighbors which are H vertices.
If any H vertex has more than \(4k\) silly neighbors just arbitrarily delete its edges to silly neighbors until it only has \(4k\) silly neighbors. There’s no reason to prefer an edge to one silly neighbor versus another. I think we just have to be a tiny bit careful because some silly vertices might be connected to multiple H vertices. That’s why we only delete edges to silly vertices for H vertices with a ridiculously silly amount of silly flexibility.
To see why this final rule is safe, imagine that initially some subset \(S\) of the H vertices were going to choose edges to silly vertices. First, for all the H vertices that had fewer than \(4k\) silly neighbors they can just take the same edges that they would have anyways. For H vertices with more than \(4k\) silly neighbors they might have to switch their choice of silly edge. But we can greedily itteratively choose silly edges for all of them. Because we left them enough flexibility. Anyways this is a polynomially sized kernel.
Proposition. Q2.8: min-ones-2-sat: is there an assignemnt with at most \(k\) ones satisfying the 2CNF SAT formula?
Proof. First do some basic cleaning: remove duplicate clauses and vacuous clauses.
“Hard Clause”: two positive variables. Obsservation: if a var occurs in more than \(k\) hard clauses, then we better set that variable to \(1\). Applying this reduction rule we get that wlog each variable occurs in at most \(k\) hard clauses.
In particular this means that there are at most \(O(k^{2})\) hard clauses, or else we can instantly REJECT.
Let \(H_1\) be the set of variables that appeaer in hard clauses. Of course \(|H_1|\le O(k^{2})\).
If we have a variable \(x\) and \(k\) distinct variables \(v_1,v_2,v_2,\ldots, v_k\) so that all the following clauses exist: \[(\overline{x}\lor y)\land (\overline{x}\lor z)\land (\overline{x}\lor w)\land\cdots,\] then we had better set \(x=F\).
We can think of some kind of recursive structure for which variable we might be motivated to set to true.
So far, the best bound I have is that there are certainly not more than \(k! \cdot k^{100}\) variables which are worth considering setting positively. So, we could pretty much forget about all the other variables.
But we want a kernel of size \(\text{poly}(k)\). Maybe I’ll see it in the morning.
EDIT: ok I have since figured out how to reduce the kernel size.
Call a variable relevant if it is implied (possibly indirectly) by some HARD variable. So like what I mean is, you can view the clause \(\overline{v} \lor w\) as the implication \(v\implies w\). And, if you have \(\overline{w} \lor u\) as well, then you get \(v\implies w \implies u\). In this case we say that \(u\) is indirectly implied by \(v\).
Anyways, suppose there is a variable \(v\) that (possibly indirectly) implies more than \(k\) other variables have to be true. Then we really can’t afford to set \(v\) to be true. So after applying this reduction we can assume that this doesn’t happen. And then we get that there are at most \(O(k^{3})\) relevant variables.
CLAIM: If there is a solution to the min-ones-2-SAT problem, then there is a solution that sets all non-relevant variables to be False.
PROOF: Suppose there is some solution. We copy the solution’s setting of relevant variables and set all non-relevant variables to False. We claim that this is still a satisfying assignment (and of course uses at most as many TRUES as the original assignment).
The only place we need to worry about is if there is a clause like \(\overline{v} \lor w\) where \(w\) is non-relevant and \(v\) is relevant. But if this clause \(\overline{v} \lor w\) actually exists, it means that \(v\implies w\). So \(w\) is actually relevant, not non-relevant.
Now that we have proven this claim we can give the kernel.
The kernel is: Apply the reductions mentioned above: namely, eliminate duplicate clauses, delete vacuous clauses, set variables which imply more than \(k\) things true to be false and set variables that are involved in more than \(k\) hard clauses to be true.
Maybe just to be careful lets also propogate clauses of the form \(v\lor v\) and \(\overline{v} \lor \overline{v}\).
And just to be precise, when I said “set a variable” in the reductions above what I mean is, set that variable to be true, and carry out all the deductions that you can from that settting.
Ok whatever. At this point we have some problem. Indentify the at-most \(O(k^{3})\) relevant variables. Set all non-relevant variables to false, and propogate stuff.
Then we are left with a formula that only involves relevant variables. So we have a formula with \(O(k^{3})\) variables. We have a trivial bound of \(O(k^{6})\) on num clauses. I think we maybe could give a better bound. But I think that’s enough for right now.
Proposition. Q2.9: can you delete k vertices to make a graph have max-degree \(d\)?
Proof. Pretty similar rules to VC. One interesting one is, you have high-deg and low-deg vtxs. And you can just toss vertices which aren’t adjacnet to any high-deg vertices.
addendum
My friend Tomas told me about a different way of looking at the kernelization algorithm for FAST.
It’s based on the following really interesting and powerful theorem about tournaments:
Theorem. If you have a tournament then you can partition the vertices into a set of maximal cycles, and then order these cycles such that each edge between an earlier cycle and a later cycle points down-wards.
Note that we have no constraint on what is allowed to happen within the cycles. Just between them.
Proof.
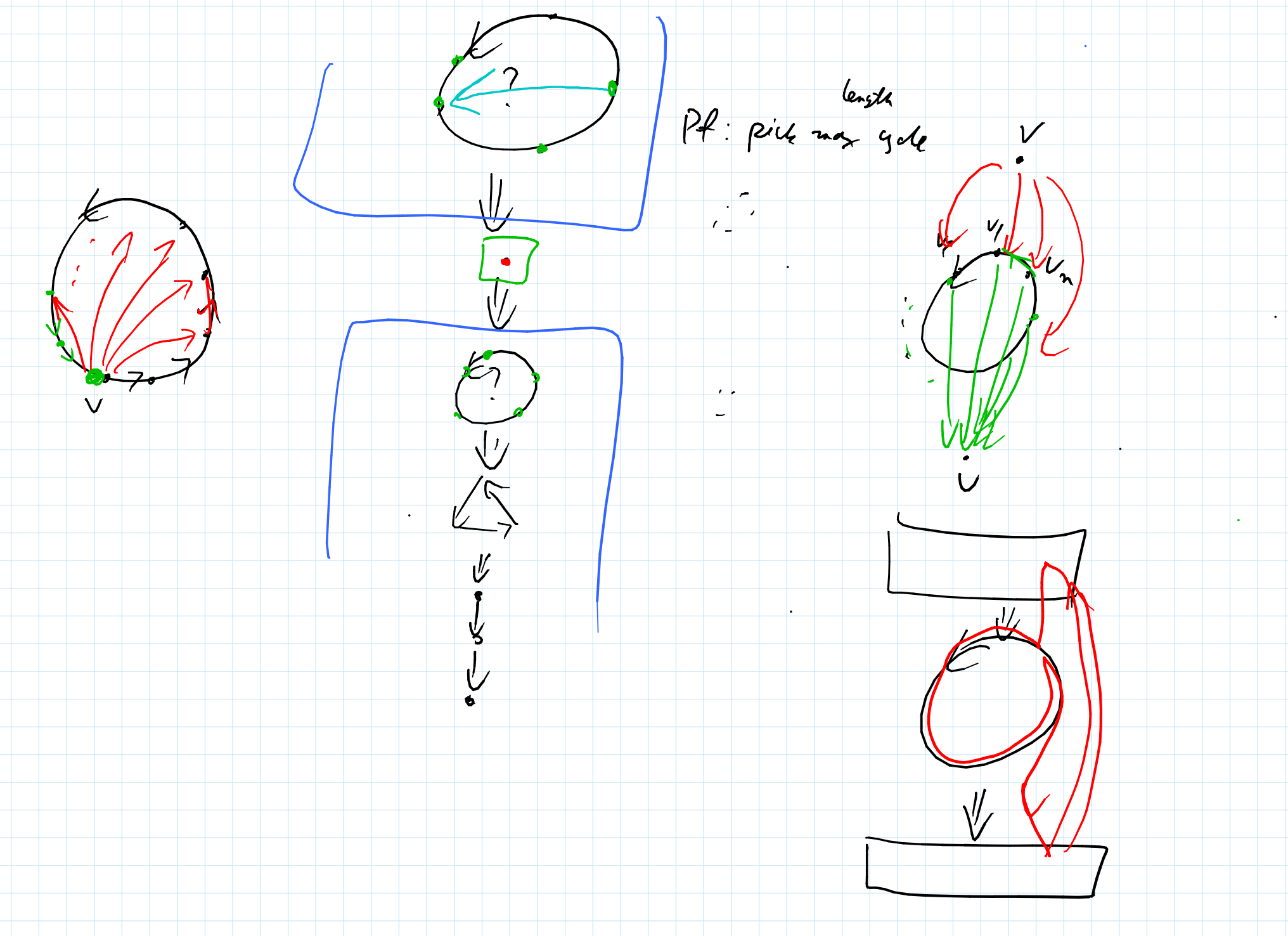
Basically, take a maximum sized cycle \(C\). If you have a vertex \(v\) with an edge to \(C\) then it turns out that \(v\) better have all its edges point towards \(C\), or else we would find a bigger cycle than \(C\). If a vertex \(v\) outside of \(C\) has an edge coming from \(C\) by the same logic all vertices in \(C\) point towards \(v\).
Finally if you had \(v\) which is below the cycle and \(w\) which is above the cycle then if you had an edge from \(v\to w\) it would create a larger cycle than \(C\).
Theorem. If you are part of one of the parts that isn’t just a singleton in the above factorization you’re contained in a triangle.
Proof. See image above