7.4 monadic logic on graphs
They define a certain logic on graphs. Let’s just write some examples.
Example.
partition: given three vertex subsets, are they a partition of the vertices of the graph?
\[\text{partition}(X_1,X_2,X_3) = \forall_{v\in V} v\in X_1 \lor v\in X_2 \lor v\in X_3.\]
indep: given a vertex subset, is it an independent set?
\[\text{indep}(X) = \forall_{u,v \in X} uv\notin E.\]
3COLOR: is my graph three colorable?
\[\exists_{X_1,X_2,X_3 \subseteq V} \text{partition}(X_1,X_2,X_3) \land \text{indep}(X_1) \land \text{indep}(X_2) \land \text{indep}(X_3).\]
Theorem. Courcelle’s theorem:
Let \(G\) be a graph with tree width \(t\), and let \(\varphi\) be a formula in monadic second-order logic. Then, there is an algorithm that determines whether \(\varphi\) is satisfied on \(G\) in runnning time \(f(||\varphi||, t)\cdot n\) for a computable function \(f\).
Remark. We can’t give good bounds on \(f\): if you alternate quantifiers a lot it can be really really really massive. Like much worse than tower. So this is more of a “if your problem is like this then its FPT” than the final word on parameterization by tree-width.
The following optimization version of Courcelle’s theorem is also useful, e.g., for vertex cover, where it’s not clear how to get a monadic formula thing that doesn’t have a \(k\) dependence.
Theorem. If you have a formula and a pretty nice function you want to optimize, that’s FPT in \(||\varphi||\) and tree-width too.
other interpretations of tree-width
path-width
Theorem. The following graph parameters are basically (up to a dumb \(\pm 1\)) equivalent:
- node-search number
- interval width
- path width
Here is a hypothetical story (not real life) to explain node-search number.
Blobby is on the run from the cops. Luckily Blobby is omniscient and has unbounded speed. He’s also invisible! Unforunately for him, the cops are really out to get him. They know his weakness: each of the cops has a box of pizza. If Blobby ever occupies the same vertex as a cop he will be sucked into the box of pizza. The cops start wherever and at each step you can do a place move: take a cop from the pool of unplaced cops and place it, or you can do a extract move: take a cop from the graph and put them into the unused cops pool.
The node-search number of a graph is the fewest number of cops needed to catch Blobby.
Here’s a picture that I think helps see why node-search number is related to interval width / path width:
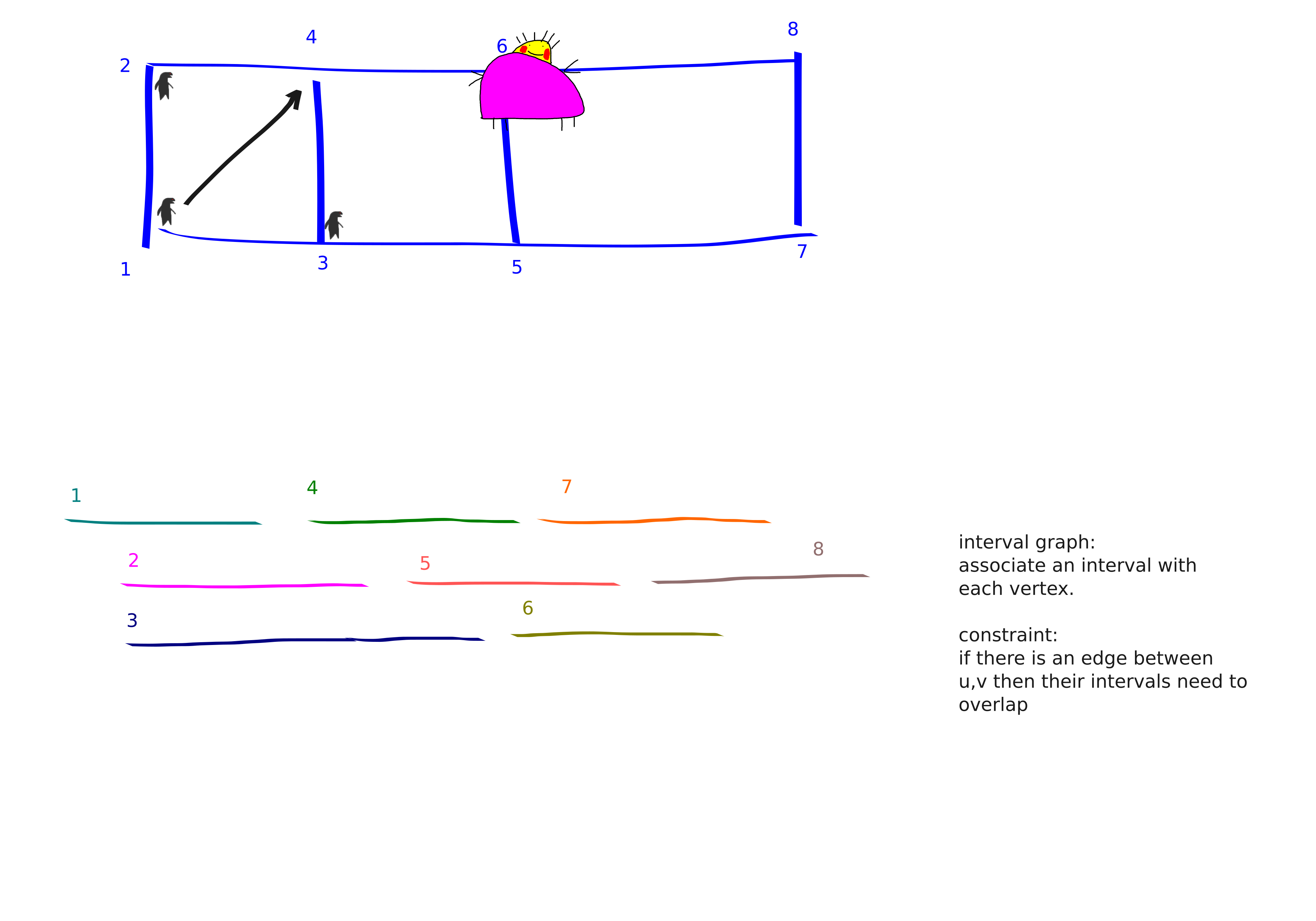
It might be hard to think of Blobby as being omniscient, unbounded speed and invisible. Instead, you can think of Blobby as being a gas that the cops are cleaning up. If there is gas on an edge it will spread to any edges that share a vertex with it, unless that vertex is blocked by a cop. If cops occupy both endpoints of an edge then the gas dies in that edge. But of course edges can be recontaminated.
tree-width
Somewhat similar story for tree-width.
Key difference: cops can see the Blobby in the tree chase version. And cops have to announce their next move, and Blobby gets to choose where to go after the cops announce move.
bramble: a collection of pairwise touching connected vertex subsets. (We say that two vertex subsets are touching if they share a vertex or if there is an edge between them).
Theorem. treewidth \(k\) iff bramble of order \(k+1\).
Proof. one direction pretty clear, other apparently very tricky.
Definition. cordal graph: Largest induced cycle is a triangle.
cordal width: min max-clique in a chordal super graph.
Theorem.
TFAE up to \(\pm 1\)
- treewidth
- chordal width
- max bramble
- cops to catch visible robber
computing treewidth
unforunately tree-width exactly NP-hard. But we can settle for FPT algo / approx algo.
Definition. \(H\) is a minor of \(G\) if you can obtain \(H\) from \(G\) by some combination of deleting vertices, edges, and contracting edges.
Remark. Apparently you can efficiently test if a constant size graph is a minor of your graph. In like \(n^{3}\) time. No idea how.
Theorem. MEME FPT algorithm for computing treewidth (i.e., determining whether treewidth is larger than \(k\) or not).
Proof.
tree-width is minor monotone: taking minors only decreases tree-width. Hence, the set of graphs with tree-width at most \(k\) is closed under taking minors. Hence, there is a set of forbidden minors, whose size depends only on \(k\), such that a graph has tree-width at most \(k\) iff it avoids the forbidden minors.
Thus, to check if a graph has tree-width at most \(k\) you just check for each of the forbidden minors whether it is a minor of your graph.
This is not such a useful algorithm maybe because determining the set of forbidden minors seems really hard, and that set is going to be freaking massive.
Remark. Ok there is also an actual (uniform) algorithm. with run time \(k^{k^{3}} \cdot n\).
But this is a bit slow, so we’re gonna just do an approx algo instead.
Theorem. There is a \(8^{k}k^{2}n^2\) algo that either constructs a tree decomposition of widdth at most \(4k+4\) or outputs (correctly) that \(G\) has treewidth larger than \(k\).
Ok, more recently: There is a \(2^{O(k)}\cdot n\) algo that either constructs a tree decomposition of widdth at most \(5k+5\) or outputs (correctly) that \(G\) has treewidth larger than \(k\).
Anyways, we’re gonna prove the easier version. But it’s looking pretty intense, so prolly has to wait till after lunch.
Before proving giving an FPT treewidth/decomposition approximation algorithm we need some graph theory lemmas.
Remark. In a tree there is a “centroid”: a vertex whose removal splits the tree into some subtrees each with at most \(n/2\) vertices.
It turns out that graphs of bounded tree-width also have “small separators”: if a graph has tree-width \(k\) there is a set of size \(k+1\) whose removal “splits the graph nicely”. We need a weighted version of this.
Lemma. separation lemma part 1:
Let \(G\) be a graph of treewidth at most \(k\) and let \(w\) be a function that assigns weights to the vertices of \(G\). Then, there exists a vertex set \(X\) of size \(k+1\) whose removal splits \(G\) into some of connnected components, each of which has weight at most \(1/2\) the total weight \(w(V(G))\).
Proof. Consider a tree decomposition of \(G\). (This isn’t circular, we’re arguing existence of a separator, not giving an algorithm for anything yet).
Arbitrarily root the tree \(T\). Find a vertex \(t\in V(T)\) satisfying:
- \(w(V_t)\ge \frac{1}{2}w(V(G))\)
- But, for any child \(t'\) of \(t\) we have \(w(V_{t'}) < \frac{1}{2}w(V(G))\)
- This can be equivalently formulated as “the furthest vertex from the root whose subtree still has half the weight of the entire graph.”
Anyways, the claim is that the bag \(X_t\) is the separator that we want.
And indeed, connected components of \(G-X_t\) either live in \(V\setminus V_t\), which we already know has less than half the weight, or in a subtree of one of \(t\)’s children, which also can’t have too much weight.
Lemma. We can find a \(2/3\)-balanced separation \((A,B)\) of order at most \(k+1\).
Proof. We use the previous lemma, form two groups of connected components in a certain way to get the balance property.
Remark. Menger’s theorem (special case of max-flow = min-cut) says that that the minimum size of a separator between two sets is the maximum number of vertex disjoint paths between the two sets. This is very algorithmic, because we can run maxflow to get separators / paths.
Corollary. If you have a vertex subset \(S\) of size \(3k+4\) in a graph with treewidth \(k\) then you can partition \(S\) into two nicely sized sets such that the \(\mu(S_A, S_B)\le k+1\).
Anyways, seems pretty powerful. Now we prove the theorem.
Proof. Assume \(G\) connected and at most \(kn\) edges.
We have a recursive procedure DECOMPOSE for constructing the decomposition.
First, we arbitrarily choose a subset \(\hat{S}\) of \(W\) with \(3k+4\) elements. Applying the corollary from above we know that there should be a partition \(S_A, S_B\) of \(\hat{S}\) such that \(\mu_{G[W]}(S_A, S_b) \le k+1\), i.e., there is a separator of size at most \(k+1\) separarting \(S_A, S_B\) in \(G[W]\). We run maxflow to try and find this separator. If we can’t find it we conclude that the graph actually has large treewidth.
Anyways, assuming we found this separator \(A,B\) with \(|A\cap B|\le k+1\) we then set \(\hat{S} = S\cup (A\cap B)\). This is going to be the root bag of our tree decomposition.
We then recursively call the DECOMPOSE procedure on all connected components that arise by deleting the root bag.
Remark. Not related to tree-width but I finally got around to fixing my image compilation script to only compile images in the file that I’m editting rather than all the images. I should probably still upgrade it to auto compile rather than manual compile. But this is a big step up: before now I was really scared to add images bc it took like 10sec to compile them. Now it’s back down to like 1sec. As I always like to say “blogging isn’t like ski rental because if someone breaks your legs you probably will end up writing more blog posts not less.”
some random treewidth related problems
Proposition. Trees have pathwidth \(O(\log n)\). And, there exists trees with pathwidth \(\Omega(\log n)\).
Proof. For the upper bound use a centroid decomposition. Let \(v\) be a centroid and let \(x,y,z\) be its neighbors (might be more or less than \(3\)). Then our path decomp is, \(v\)’s interval spans the whole way, but then we do \(T_x\)’s interval graph, followed by \(T_y\)’s and followed by \(T_z\)’s.
hmm, the book claims that it’s non-obvious that there are trees with pathwidth \(\Omega(\log n)\). But it seems to me that it’s pretty clear that e.g., binary trees have \(\Omega(\log n)\) pathwidth. Not exactly sure how to prove though.