Proof.

First we show how to take \(2\) dominance products and then do \(O(n^{2})\) work to combine their output into the answer to the equality product. It’s quite straightforward: Count the number of \(k\) so that \(A[i,k]\le B[k,j]\) and also the number of \(k\) so that \(A[i,k]\ge B[k,j]\). Add these numbers and subtract \(n\). This results in the number of double-counted numbers which are precisely the equality cases.

Now for the more difficult dirrection.

We take a Dominance product instance and convert it into \(O(\log n)\) equality product instances, whose sum is the dominance product.

We consider the numbers to be integers in the range \([0,n^{O(1)}]\). Let \(L\le O(\log n)\) be the maximum number of bits in any of the numbers. From now on we think of the numbers as all being \(L\) bits, padding with zeros as necessary.

For each \(\ell \in [L]\), form matrix \(A_\ell\) by taking the \(\ell\) most-significant bits of each entry in \(A\). Define \(B_\ell\) as the \(\ell\) most-significant bits of each entry in \(B\), except: if the \(\ell\)-th most-significant bit is a \(1\) then replace the number with “\(\bot\)” (i.e., some symbol that isn’t allowed to match with any values in \(A_\ell\)). If the \(\ell\)-th digit is a \(0\) then replace this \(0\) with a \(1\).

It’s evident that this is basically just an \(L\)-overhead compared to the equality product. Why does it work though?

The idea is, if \(A[i,k]\le B[k,j]\) then we will count a point towards \((A \star_\le B)[i,j]\). In particular, we will count this point on the matrices \(A_\ell, B_\ell\) for \(\ell\) being the index of the first bit on which \(A[i,k], B[k,j]\) differ.

The intended solution in Virginia’s class pset2 is different. But I’m pretty sure that what I did works too.

Proof.

For \(i,j\in [n]\) let \(a_i\) denote the \(i\)-th column of \(A\) and let \(b_j\) denote the \(j\)-th row of \(B\).

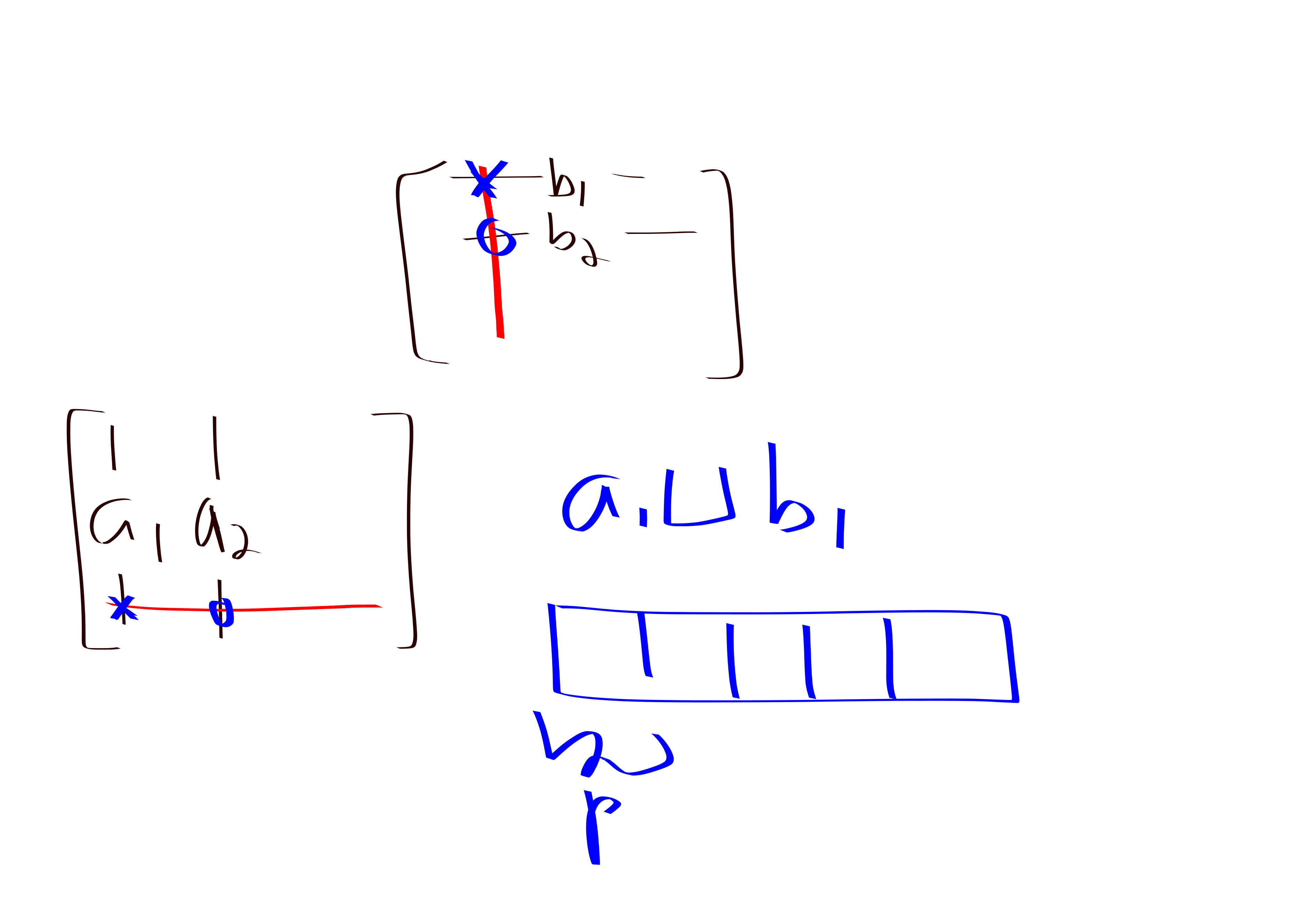
For each \(j\), sort \(a_j\sqcup b_j\). Fix parameter \(p = n^{(\omega-1)/2}\in [n^{.5}, n^{.7}]\). Define buckets \(S_{j,1},S_{j,2},\ldots, S_{j,2n/p}\) to be contiguous chunks of \(a_j\sqcup b_j\) with size \(p\).

For each \(i,j\) record $H_{i,j} = $ which \(j\)-bucket \(A[i,j]\) was placed in. Similarly, for each \(j,k\) record $G_{j,k} = $ which \(j\)-bucket \(B[j,k]\) was placed in.

Now, for each \(b\in [2n/p]\) form matrices \(A_b, B_b\) where \(A_b[i,j]\) is \(1\) if \(A[i,j]\) was placed in bucket \(S_{j, b}\), and \(B_b[j,k]\) is \(1\) if \(B[j,k]\) was placed in a bucket \(S_{j,b'}\) for some \(b'>b\).

Then, the integer matrix product \((A_b B_b)[i,j]\) counts the number of \(k\) such that \(A[i,k]\le B[k,j]\) and \(A[i,k]\) is in bucket \(b\) and \(B[k,j]\) is not in bucket \(b\).

Summing over all values of \(b\) gives the number of \(k\) so that both \(A[i,k]\le B[k,j]\) and \(A[i,k], B[k,j]\) are in different \(k\)-buckets.

Finally, we brute force over all pairs of elements in each of the buckets. There are \(O(n^{2}/p)\) buckets and \(p^{2}\) pairs of elements in each bucket. This makes for \(O(n^{2}p)\) checks that we need to do here. Like, the check that we are doing is for each pair we adjust whichever product involves the both of them appropriately.

Anyways, the running time of this thing is \[(n/p)n^{\omega}+n^{2}p \le n^{(\omega+3)/2}.\]

Proof. Its also by bucket and brute force, similar to the dominance product one.