Remark. In this blog post \(O\) generally means “ignoring both constants and logarithmic factors”. I’m not saying log-shaving isn’t interesting here. It could be. Just not atm.
new: summarizing Dor, Halperin, Zwick’s additive \(+k\) approx in \(n^{2+1/k}\) time.
I have been known for introducing lots of notation. It’s a bad habbit that I’m trying to cut back on (with the exception of using \(\perp\) to denote \(\gcd\) which is the one exception I will allow myself). This paper by Dor Halperin Zwick is so clear and beautifully written. The only thing I can say about it is including this screenshot. And maybe writing the analysis that they omitted of why this algo works. (The analysis is in a later paper, “Cohen, Zwick, All pairs small stretch paths”. I might also dig up that paper.)

One really interesting thing is that they claim that this algorithm is a \(\cdot 3\) approx, not just a \(+k\) approx. That is pretty overpowered.
lower bound
Theorem. Suppose you were really clever and thought you found a really fast \(\cdot 1.9\) approximation algorithm for APASP, where fast means faster then matrix multiplication. Then actually that’s impossible.
Proof.
I’m not really sure what SotA is for directed APSP approx. But here’s a construction I came up with: 
I think this shows \(*2\)-approx is impossible for any constant length path. it would be extremely interesting if some lower bound like this held for undirected paths of length 3. it probably doesn’t tho.
some APSP stuff
weird idea:
- if two vertices have a really long shortest path between them, them you can take a hitting set of size large enough that it’ll hit a vertex on the path :O. Now that’s crazy.
- if two vertices have a fairly short longest path between them then you can catch it with MM.
Proposition. You can do APSP in directed unweighted graphs in \(n^{(\omega+3)/2}\) time.
Proof. Throughout proof \(c=2.37\) denotes the current best value of \(\omega\). Set \(k=n^{(3-c)/2}\approx n^{.35}\). Find short long paths in time \(kn^{c} \approx n^{2.7}\) just via successive MM. Do hitting sets for paths of length longer than \(k\) which costs \(n^{3}/k \approx n^{2.7}\).
Overall cost is \(n^{(3+c)/2}\).
This might seem supa slow. But it’s impressive that it handles directed graphs: directed graphs are pretty hard.
Seidel’s Algorithm
Now we focus on undirected graphs, and give an \(O(n^{\omega}\log n)\) algorithm.
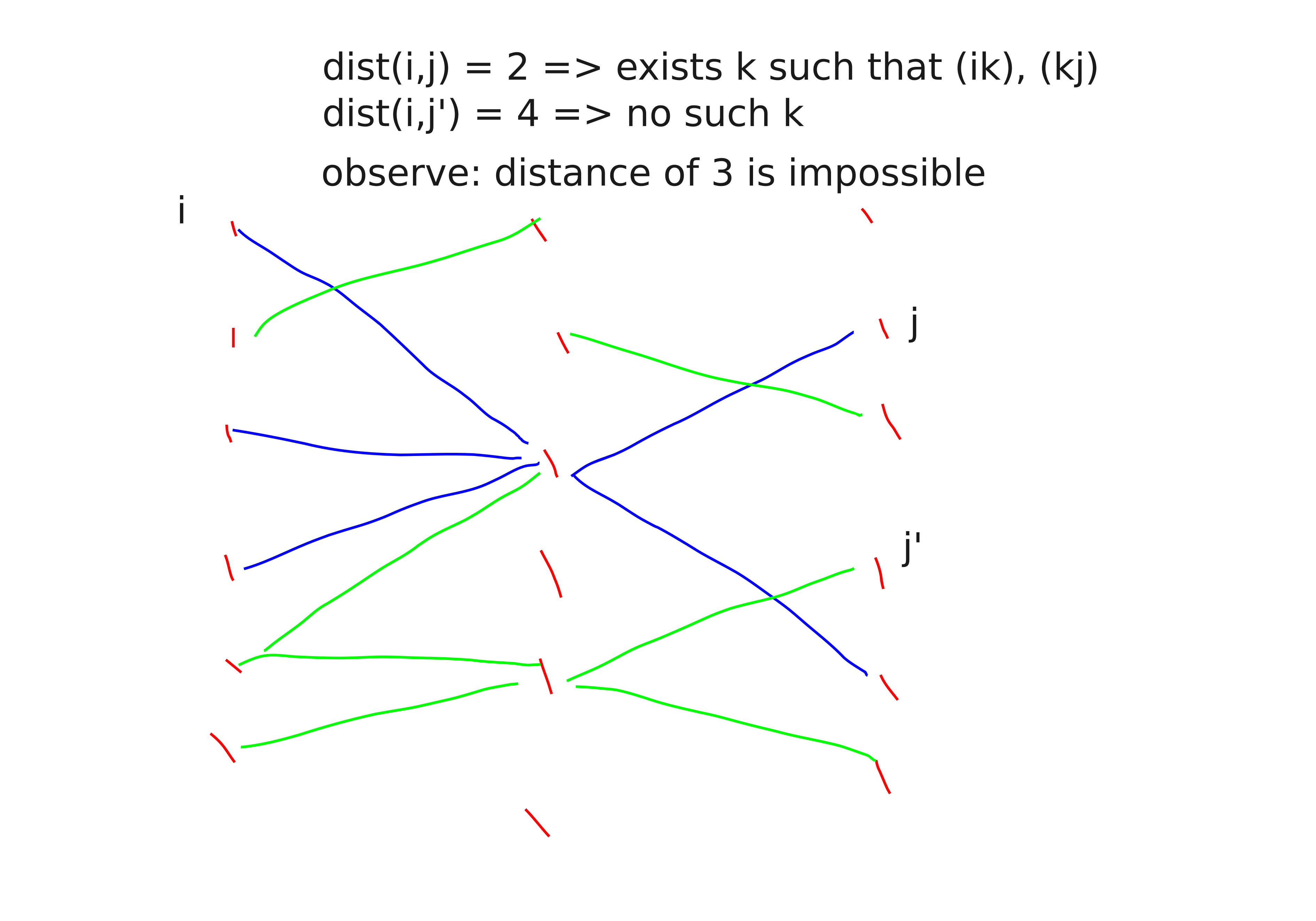
interesting observation: Suppose that \(u\) is a neighbor of \(v\). Then for any other vertex \(w\) we have \(d(w, v) \in d(w, u)+[-1,1]\). In particular \(d(w,v)\equiv d(w,u)\mod 2\implies d(w,v)=d(w,u)\).
I think this is important in Seidel’s \(O(n^{\omega}\log n)\)-time APSP alg. Like I think his alg is you repeatedly square the adjacency matrix and then some how compute parity of path lengths using some corollaries of the above observation and MM.
additive graph spanners
Theorem. +2 spanner with \(n^{3/2}\) edges.
Proof. So a graph spanner is a (hopefully) sparse subgraph that approximately preserves distance information.
This one is exactly what you would expect: keep edges incident to vertices of degree smaller than \(\sqrt{n}\), and take all edges out of a random hitting set of size \(\sqrt{n}\).
Remark. Let \(P\) be a shortest path. Then any vertex has at most \(3\) neighbors on \(P\).
Remark. If shortest path \(P\) has at least \(L\) nodes of degree at least \(D\) then there are \(\Omega(LD)\) distinct neighbors of the path \(P\).
Remark. Very interesting: [due to Abboud]
There exist graphs that don’t admit \(n^{4/3-\varepsilon}\) edge spanners with additive error \(+\mathcal{O}(1)\).
In fact, there are graphs such that any \(n^{4/3-\varepsilon}\) edge subgraph has additive error at least \(n^{\delta}\).
Theorem. There is a \(+4\) spanner with \(O(n^{7/5})\) edges.
TODO: It is open whether you can do \(n^{4/3}\) here.
Proof. We have two parameters: \(L, D\). \(D\) is a degree threshold: higher than D degree is high degree, lower than \(D\) is low degree. L is a number of high degree vertices on a path before we consider that path fancy.
Our spanner is as follows: (rmk this is existential not an algo)
Let \(S\) be of size \(n/D\) be a hitting set for high degree vertices. Let \(T\) be of size \(n/(DL)\) be a hitting set for fancy paths. (i.e., every fancy path has a neighbor in \(T\)). For high degree vertex \(x\) let \(r(x)\) be the representative of \(x\) in \(S\). i.e., an arbitrarily chosen neighbor of \(x\) in \(S\).
- Take all edges incident to low degreee vertices. Cost \(nD\)
- Take full BFS trees out of all vertices in \(T\). Cost \(n^2/(DL)\).
- Take \((x, r(x))\) edges for each high degree \(x\).
- For each pair of distinct vertices \(s,s'\) in \(S\), let \(P_{s,s'}\) be the set of all non-fancy shortest paths between a neighbor of \(s\) and a neighbor of \(s'\).
- Let \(p^{*}\) denote the shortest path in \(P_{s, s'}\). Add edges from the endpoints of \(p^{*}\) to \(s,s'\) based on where the endpoints of \(p^{*}\) came from.
- Now take all the edges in path \(p^{*}\). I guess you don’t need to take edges that we’ve already taken, in particular, let’s not re-take edges touching low degree vertices.
- With this convention the total number of edges taking to do this \(s,s'\) link is \(O(L)\).
- Thus overall this step takes \(O((n/D)^2 L)\) edges.
Set \(L=n^{1/5}, D = n^{2/5}.\) Then this is the desired sparsity.
claim this is a \(+4\) spanner. proof:
It’s pretty clear that this can take care of fancy paths and take care of paths with no high degree vertices. Remaining case is paths with non-zero, but also non-alot many high degree vertices. This is explained in the following picture.
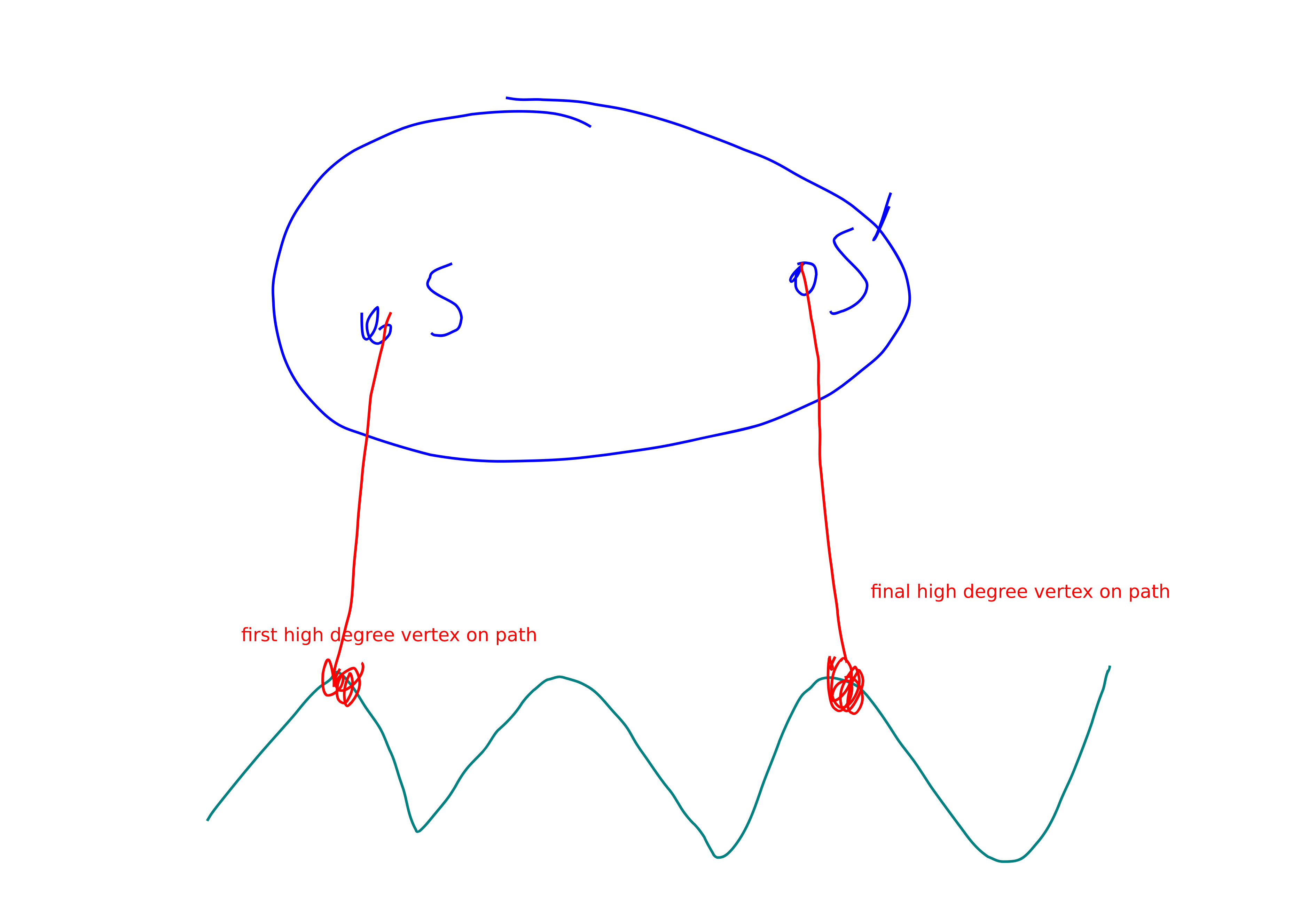
Theorem. There is a \(+6\) spanner with \(O(n^{4/3})\) edges. Clearly by the remark above you can’t hope to do any sparser than this.
TODO: read this it seems cool
multiplicative graph spanners
Theorem. Every \(n\) vertex graph contains a \((2k-1)\)-spanner (multiplicative approx to distances) with \(O(n^{1+1/k})\) edges. This is tight assuming Erdos girth conjecture.
TODO: read this it seems cool