remarks before the survey
Remark. This paper uses the convention I dislike for \(k\)-paths, i.e., they call a path with \(3\) edges a \(P_4\). I do not adopt this convention. For me a path with \(3\) edges is called a \(P_3\). You have been warned.
Remark. “Universal algorithm for induced SI”: \(n^{k\omega}\) time to detect a \(3k\) vertex pattern.
You compute this huge \(3\)-partite graph where vertices are labelled \(k\)-vertex subsets. Then you run triangle detection on this massive graph.
Theorem. Combinatorial \(O(n^{k-2})\) algo for induced \(P_k,C_k\) problems.
Theorem. For a couple specific values of \(k\in [5,9]\) they are able to boost the MM based algo for \(P_k,C_k\)’s by doing their arithmetic circuits with matrices. But they weren’t able to get this in full generality.
Remark. Oh, apparently Virginia had some algorithms for, e.g., \(K_k-e\) that run in time \(O(n^{k-1})\). Worth reading at some point.
Seems like these guys also do something impressive about SI nk-1 SI for lots of graphs they prove some conditional lower bounds too.
Maybe also relevant is the paper “Finding Four-Node Subgraphs in Triangle Time” where Virginia et al show how to do all \(4\)-vertex patterns.
introduction / motivation
A very cool and very classic algorithm that I’ve discussed previously on this blog is Ryan Williams’ \(k\)-path subgraph isomorphism algorithm.
I may have just stated it for hamiltonicity, but it works for general \(k\).
The idea is as follows. You write down a polynomial with terms corresponding to possible homomorphic copies of the pattern in your graph. And then you hope that it’s easy to evaluate and that whether or not it is identically zero can tell you something about it.
Ok, you might say, but what does this have to do with induced paths/cycles?
You can write some polynomial like this:
\[ I_{P_3,n} = \prod_{a,b,c,d\mid a<d} x_{a,b}x_{b,c}x_{c,d} (1-x_{a,c})(1-x_{a,d})(1-x_{b,d}) \]
Here’s a picture of expanding this: 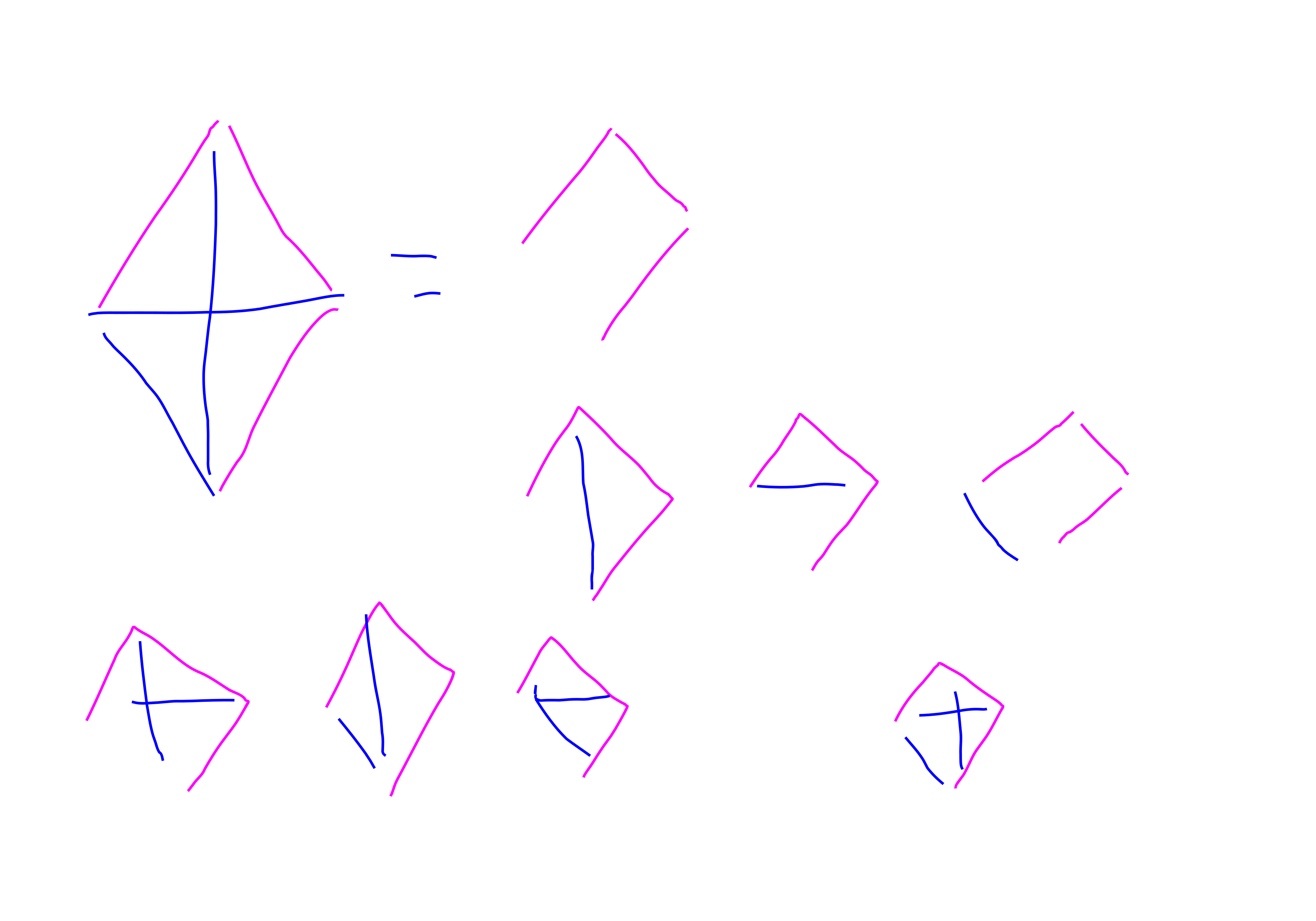
Then you expand this polynomial out and look at it modulo \(2\). You get \[ I_{P_3,n} \equiv N_{P_3,n} \mod 2.\] So this is rather suprising. There are a lot of scary looking terms that drop out when you take the mod.
\(N_{P_3, n}\) is the polynomial for not-necessarily induced \(P_3\)’s.
note to self: section 6 looks particularly relevant. sections 3,4 seem to be prerequisite to understanding any of this stuff.