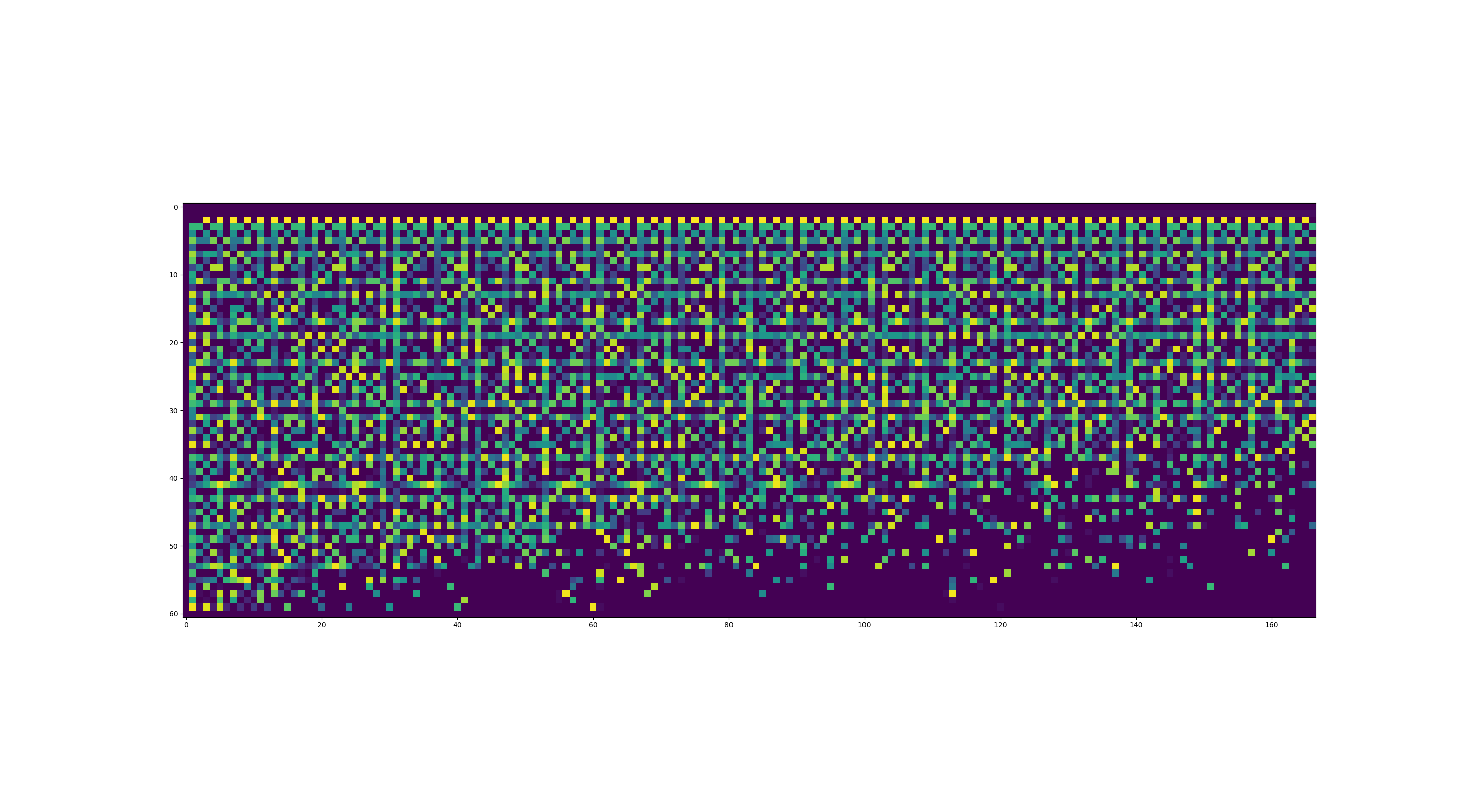
Lately, my favorite “fact”, (I’m at least 95% true that I have a correct proof of this statement, although have not writting it up super carefully) is the following:
Theorem. Let \(x\in [\frac{p}{2}]\). Then there exist \(m\le n\) and \(k\) with \(|k| \le \frac{p}{n}\) (where by \(|k|\) I mean \(\min(p-k, k)\)) such that
\[x \equiv m^{-1}k \mod p.\]
What this means is, you can take any \(x\in [p]\) and break it down into two parts: a part of size in \([n]\) and a part of size in \([\frac{p}{n}]\).
I think this is super cool.
PS: If it’s not true, or if it is well known and you have a citation for it, please let me know.
The proof sketch is as follows: - for concreteness think of \(x\) as being some size, like maybe \(\approx \frac{p}{i}\) . - So like after \(i\) steps you wrap around once. And (assuming \(x\) didn’t already start super small), this wrap around thing will be pretty small, like less than \(\frac{x}{2}\) say. - keep going for a bit and you can get it down to \(\frac{x}{3}\). - You just do a bunch of balancing arguments to say that you’re making progress.
Anyways, this blog isn’t about a proof. It’s just because I made a cool picture of \(x(m,k)\), see the heatmap above. Enjoy!
- EDIT 1: oops the picture literally proves that my above “theorem” is somewhat false. well, sigh, happens.
- EDIT 2: ok I modified the “theorem” to say \(x\in [\frac{p}{2}]\) is uniquely represented by \(m,k\). Now, this is not in contradication with any observed data. Still worth being cautious though.
- Edit 3: ok here’s what is actually the case:
Theorem. For each \(x\in [p]\), there exists \(m\le n, k\le \frac{p}{n}, \sigma \in \pm 1\) such that \[x \equiv \sigma m^{-1}k \mod p.\]
Proof. This is true by the pidgeon hole principle:
It you look at \([n]x\) it must have two poitns \(i,j\) with \(xi,xj\) close. So then if we define \(k=|i-j|\) we have the desired property.
So basically, above I was on the right track, but I got side-tracked by trying to say that the representation was unique, which doesn’t make any sense and is also false.