Anthropic put out a paper a while ago about superposition, I thought it was a very nice read, and the findings were surprisingly elegant. It’s cool when things make sense!
Here are some notes I wrote while reading it.
my own experiments
I spent a few minutes to code up some of the most basic experiments described by Anthropic.
edit:
I worked on debugging why I was having trouble reproducing Anthropic’s superposition.
I’m not actually sure what I changed, but using Adam with
I think setting up variable importances also mattered a bit for getting this result. If you don’t do this I could imagine that the model would just come up with some scheme for counting the number of inputs turned on or something.
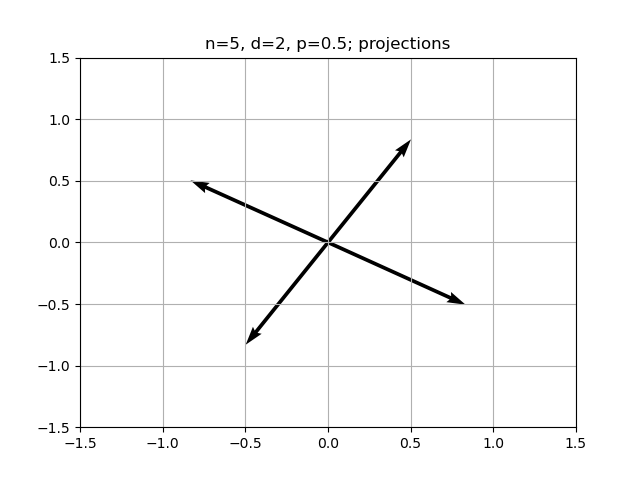
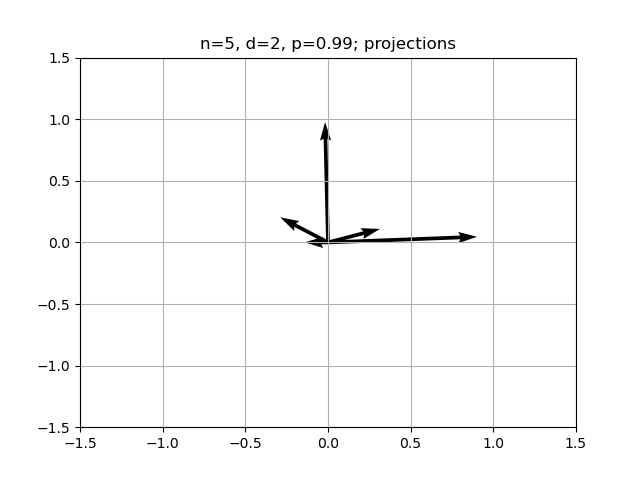
Ah yeah nice I’m starting to get the same plots as Anthropic
Here’s a picture of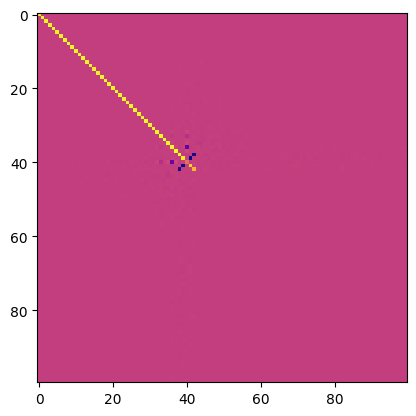 
The setup is the early variables are the most important, and importance drops off exponentially.
The dot products show how much interference there is between the features.
I tried doing a graph of where the strong connections are.
I don’t think I’m quite setting this up correctly. But I do see some antipodal pairs like they claimed that you’re supposed to, so that’s at least good.
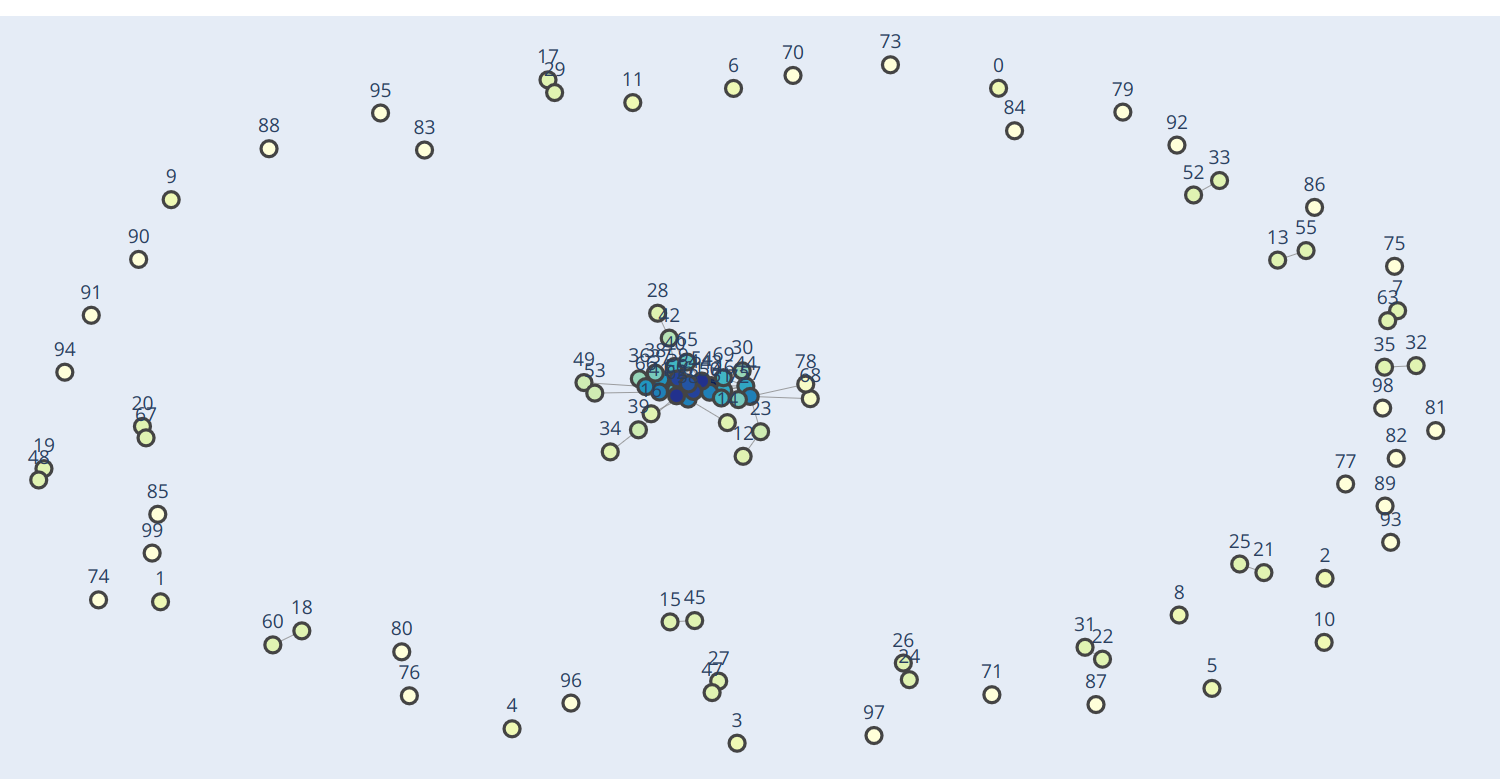
ok this graph turned out much nicer: I didn’t plot the degree one guys just for sake of clarity. I’m not really sure why there aren’t any structures besides the dipole guys. I guess maybe it’s not the correct regime for these other things to emerge in.
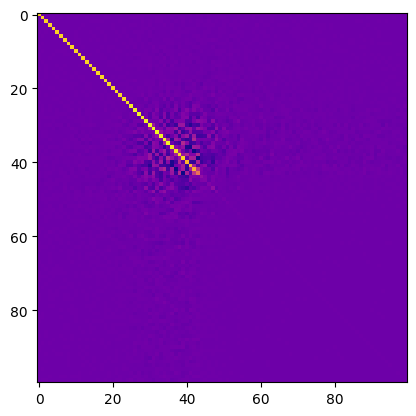
(todo: hmm, I thought these were supposed to be orthogonal? They’re close to orthogonal, but not quite.
I guess it’s far enough apart that it’s not an issue.
Also the anti-podality is perfect. )
(this one is a bit weird; it’s supposed to only get two directions. I think this is a failure of the optimization; probably two directions would be lower loss? TODO: check whether that’s actually true.)
"""
INPUT:
x, sampled from Ber(p)^n*Unif(0,1)^n (indep rvs)
W: project x down to a d dimensional space
d << n
but maybe p*n \approx d
Loss = MSE( Relu(W^T W x + b), x )
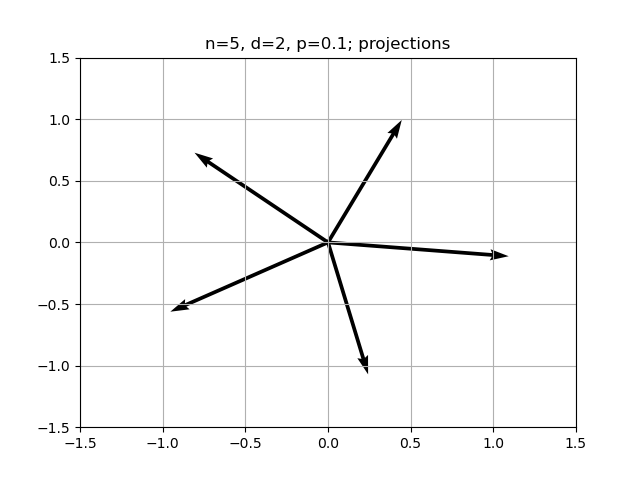
First test:
Let n = 3, d = 2,
Vary p
PLOT: projections of each feature
conjecture: if p is small enough, should get a triangle
"""
import numpy as np
import torch as t
from torch import nn
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt
# Generate independent data from Bernoulli(p)^n * Unif(0,1)^n
def gen_indep_data(N, n, p):
return t.bernoulli(t.full([N, n], p)) * t.rand((N, n))
class MLP(nn.Module):
def __init__(self, n, d):
super(MLP, self).__init__()
self.W = nn.Parameter(t.randn(d, n))
self.bias = nn.Parameter(t.zeros(n))
self.relu = nn.ReLU()
def forward(self, x):
hidden = x @ self.W.T
activation = self.relu(hidden @ self.W + self.bias.unsqueeze(0))
return activation
n = 5
d = 2
p = 0.1
# Generate data
data = gen_indep_data(10_000, n, p)
dataset = TensorDataset(data, data)
dataloader = DataLoader(dataset, batch_size=64, shuffle=True)
# Model, loss function, and optimizer
model = MLP(n, d)
criterion = nn.MSELoss()
optim = t.optim.Adam(model.parameters(), lr=0.001)
NEPOCHS = 40
for epoch in range(NEPOCHS):
epoch_loss = 0
for batch_data, _ in dataloader:
optim.zero_grad()
output = model(batch_data)
loss = criterion(output, batch_data)
loss.backward()
optim.step()
epoch_loss += loss.item()
print(f"EPOCH: {epoch+1}/{NEPOCHS}, \t LOSS: {epoch_loss}")
# Plot the projections
W = model.W.detach().numpy()
for i in range(n):
ei = t.zeros(n)
ei[i] = 1
vec = W @ ei.numpy()
plt.quiver(0, 0, vec[0], vec[1], angles='xy', scale_units='xy', scale=1)
plt.title(f"n={n}, d={d}, p={p}; projections")
plt.xlim(-1.5, 1.5)
plt.ylim(-1.5, 1.5)
plt.grid(True)
plt.show()
mmm, then I tried to do this with more dimensions. It is not working the way I thought it should. #todo debug this…
"""
INPUT:
x, sampled from Ber(p)^n*Unif(0,1)^n (indep rvs)
W: project x down to a d dimensional space
d << n
but maybe p*n \approx d
Loss = MSE( Relu(W^T W x + b), x )
Second test:
Let n = 100, d = 40,
Vary p
TODO1: check mathematically what the optimal bx should be for p=1
psure anthropic said that in this case it should just choose a few coordiantes to focus on. wait p=1 is ridiculous?
Maybe the thing to look at is cosine similarities of projections. yeah sure seems good.
conjecture: cosine similarities should be pretty sparse for some range of p (the little local superposition things.)
"""
import numpy as np
import torch as t
from torch import nn
from torch.utils.data import DataLoader, TensorDataset
import matplotlib.pyplot as plt
# Generate independent data from Bernoulli(p)^n * Unif(0,1)^n
def gen_indep_data(N, n, p):
return t.bernoulli(t.full([N, n], p)) * t.rand((N, n))
class MLP(nn.Module):
def __init__(self, n, d):
super(MLP, self).__init__()
self.W = nn.Parameter(t.randn(d, n))
self.bias = nn.Parameter(t.zeros(n))
self.relu = nn.ReLU()
def forward(self, x):
hidden = x @ self.W.T
activation = self.relu(hidden @ self.W + self.bias.unsqueeze(0))
return activation
n = 100
d = 40
p = .01
# Generate data
data = gen_indep_data(10_000, n, p)
dataset = TensorDataset(data, data)
dataloader = DataLoader(dataset, batch_size=64, shuffle=True)
# Model, loss function, and optimizer
model = MLP(n, d)
criterion = nn.MSELoss()
optim = t.optim.Adam(model.parameters(), lr=0.001)
NEPOCHS = 50
for epoch in range(NEPOCHS):
epoch_loss = 0
for batch_data, _ in dataloader:
optim.zero_grad()
output = model(batch_data)
loss = criterion(output, batch_data)
loss.backward()
optim.step()
epoch_loss += loss.item()
print(f"EPOCH: {epoch+1}/{NEPOCHS}, \t LOSS: {epoch_loss}")
# Plot the projections
W = model.W.detach().numpy()
plt.imshow(W.T @ W)
plt.title(f"cosine similarities of feature projections")
plt.show()
Notes on their paper
anthropic superposition in toy models paper
Features — meaningful directions in activation space.
Linear representation hypothesis:
There are features, which might or might not be present.
Hopefully they are often not present (sparsity).
The features can have values, and the hypothesis is that the activation on a sample is basically something like
- they’re quite simple
- they’re “easily selectable” — in a single linear layer thing you can do a projection to get the value of a feature (if it’s linearly represented) and then use this to decide whether to activate or not.
I think the geometry / graph part of this paper is super cool.
I think the best way to understand this is to go look at their pictures. But I’ll summarize below to make sure I understand.
The setup:
We have 10 features. But only 2 dimensions.
The features are equally important.
At the end we’re going to be asked to reconstruct the input vector, and penalized with MSE.
For now assume that the features are all present or not independently with some probability
each. Messing with the relative probabilities is interesting, and introducing correlations is also interesting, but we’ll get to that later. First, suppose or something. Then nothing interesting happens — the model will just orthogonally represent two of the features. Ok, but what if got smaller? - After a while the model will start to represent things anti-podally.
- At lower sparsities the model tries shapes like tetrahedrons,
- pentagons, and square antiprisms
- There are some mathematical reasons why these shapes are good — these shapes also occur in chemistry — it’s some kind of “what’s a nice way to spread things out” question.
- A note of caution — when you have a shape like a triangular bipyramid, the strengths are not symmetric.
- There are sharp phase transitions for what geometry the model chooses to use to represent stuff with.
- At least at first, if you have a bunch of features the model will only make little tiny islands of superpositioned things. What if you had non-uniform importance?
- sometimes deforms shapes
- sometimes shatters them What about correlated features:
- positively correlated:
- orthogonal good
- close ok
- negatively correlated
- antipodal good Sometimes, if features are highly correlated, a PCA-like strategy makes more sense. OpenQ: understand the tradeoff here.
discussion of learning dynamics
- they study how the solutions evolve over time
- find that it’s “surprisingly discrete” / phase-changey
- and that the model learns these things one thing at a time.
Adversarial Examples
- superposition seems to possibly play a role in causing lack of robustness
- They say that the reason why is that the first col of
is instead of . Maybe the point is usually the ‘s are supposed to cancel out as noise, but an adversary could choose not to do this?
computing in superposition
- superposition isn’t just for storing stuff
- model can learn to do computations in superposition as well.
motivation
- ok, now I think they’re going to talk about how mech interp is good for solving alignment
- idea: if you can identify all the features in your model, and there is a “be evil” feature, then maybe you should be concerned if this activates? The basic idea is that solving superposition (which maybe SAEs do?) let’s you break up activation space in nice ways.
Proposing some solutions
- Maybe there are models that don’t exhibit superposition but are still competitive. Mixture of Experts was proposed.
- apparently in mixture of experts you can have a bunch of neurons, but only a few experts activate on any given query. and then you can not expend FLOPs on the neurons that aren’t activating.
- so maybe such models don’t need superposition
SAEs
Now I’m going to take a look at another seminal paper — about SAEs. https://transformer-circuits.pub/2023/monosemantic-features/index.html
Features split when you let more of them exist.