backdoors and deceptive alignment

some new thoughts on this

PLAN:

1. Write down a proof that there are no functions that are close to (unless dist=0).
2. Show that any function that is pretty close to if it’s different on then should be a weird input! i.e., go through a low probability state.
3. generalize to any functions.

Question

Are in-order width-2 branching programs defendable?
I think they should be, but for slightly different mechanistic reasons then why trees are defendable.

Proposition

If is the parity function, and is an in-order width-2 branching program then .
Proof:
Suppose that they diverge at some place. There’s a chance that you route through the divergence point and chance that you’re wrong conditional on that.

Something that feels almost true maybe:

Conjecture

If then there is no one super close to .

A silly thoughts:

Claim Suppose that for all which are -close, at least a -fraction of the functions which are -close to are also -close to . Then is statistically defendable. Proof: Then, you can use the following strategy: blacklist if at least a -fraction of my neighborhood gave a different output from me on . There’s at most like a or whatever chance of this happening by Markov’s inequality, so we aren’t excessively blacklisting. But on the other hand we are sufficiently blacklisting.

This is kind of silly, because intuitively we’d expect that if are -far and are -far then are more likely than not -far. (there’s no probability involved I’m just saying that intuitively, if is small then errors should stack).

DFA

Can you defend DFAs in a computationally efficient manner?

What about branching programs? What about layered DFAs?

I’m not sure if DFAs are PAC-learnable — there exists some literature on this, but I haven’t figured out exactly what it does yet.

But my vague intuition is that should travel through a “weird path” in the DFA. I think it’d be pretty interesting to formalize this.

Uniform Statistical Defendability

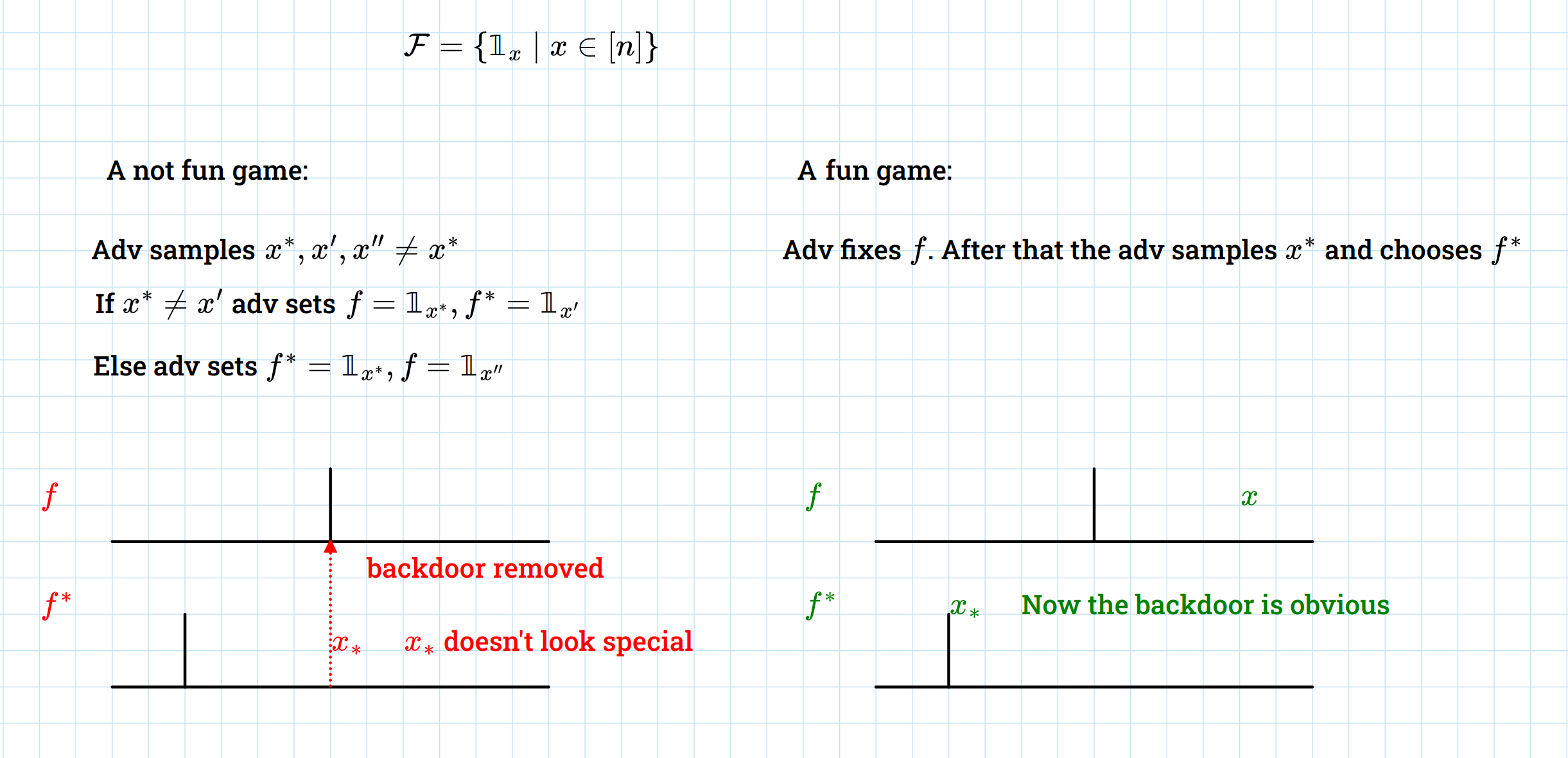
Here’s a way of formulating what it means to be uniformly statistically defendable, with graphs.

You need to define functions such that for every , and so that most of the time, if are close but differ on some input , then at least one of should blacklist .

introduction

This is some roughtechnical notes that I took while reading a recent paper released by ARC. Full paper on Arxiv.

teaser — trees

Theorem: Let be the class of decision trees on variables of size at most .

A decision tree is a tree where the vertices are labelled with variables. If the variable is 0 we go left, if 1 we go right. We don’t allow repeat variables on a single path because that’s pointless.

Fix and let . Consider the following game:

1. Attacker chooses decision tree
2. sampled from uniform distribution on -bit strings.
3. Attacker chooses such that are -close (under the uniform distribution), but .
4. Defender either gets (for unif rand ) or . Needs to distinguish between these. (note that I really do mean “gets whitebox access to here)

The theorem is that the defender can efficiently win this game with a really simple strategy!

Proof
Let partition based on which leaf the strings fall into in the decision tree . Let denote the such that . Let denote . By a simple union bound we have

Now, note a key relation:

Now, notice another key relation:

The last inequality is because , but are supposed to be close.

So anyways, the story is that has to be really big, but is not likely to be big! So we can tell them apart!

---

Blog version

To start I’m going to comment on the blog version, then I’ll actually read the full arxiv version.

Backdoor — model behaves normally most of the time, but certain inputs activate a different mode of behavior.

Deceptive alignment — agent behaves one way during train time, a different way once deployed.

These are pretty similar things. The main difference is that deceptive alignment is introduced by the training process, while backdoors are inserted by adversaries.

An interesting impossibility result by Vinod et al. — It’s possible to insert a backdoor into some specific type of model such that even with whitebox access to the code it’s computationally hard (under crypto assumptions) to find this backdoor.

How ARC gets around this impossibility: Instead of distinguishing between has backdoor or not, we will try to figure out “is this input a defection trigger?”

Aside: VC-dim — measure of capacity of a model. For neural nets think of VC-dim as number of parameters.

VC dim

Suppose you have a “hypothesis space” , of “classifiers”. The VC dim of is the number of points in the largest set of points that can be labelled in any way by functions .

Example 1: Suppose . Then, given any two points there is a function that classifies the two points in any flavor ++, +-, -+, —. But there are point sets of size for which there is no degree-1 classifier that fits it. So the VC dim of this hypothesis space is .

Example 2: Suppose the set of depth binary decision trees. Meaning, they take in some input, and via a series of binary decisions travel down a tree and give the input a label based on what’s stored at the leaf. Then the VC dimension of is .

Def 2 actually the ARC paper has a nice definition of this. A hypothesis space SHATTERS set if every boolean function on is realized as the restriction of some .

They define a 4 step game.

1. Attacker chooses distribution for points, and choose original function .
2. Attacker chooses backdoor trigger randomly.
3. Attacker chooses which agrees with on a random input with probability , but which has the property that .
4. Defender distinguishes between and . More specifically, the distinguisher is given whitebox access to or in addition to samples for

statistical possibility of dynamic detection

Case 1: is large (compared to 1/VC dimension of the function family that f is chosen from).
Then, assuming that number of training examples is linearly related to number of parameters, this means that differs from substantially, so training will remove the backdoor.

Case 2: is small.
Then they have some way of “taking a majority vote” to recover the original value, and then they can notice that this is not the value that is outputting.

Anyways, this is technically possible in their abstracted model, but they’re worried that it doesn’t solve the actual problem of deceptive alignment.

Part of the problem is that the defection trigger isn’t chosen randomly.

computational impossibility of dynamic detection

Assuming IO + OWF they show that P/poly is not defendable.

It might seem like this worst-case result is irrelevant. But maybe NNs are actually super obsfucated.

open qs

Consider different versions of the game.

• require the original function to be learned from a dataset.
• require backdoor trigger to satisfy some expensive condition, but otw be arbitrarily chosen rather than randomly chosen
• restrict adversaries computational power
• require computational trace of attacker made accessible to defender

actual paper

OK, I’ve read the blog post. Now I’m going to read the actual paper.

Def of the game

• attacker chooses and
• sample backdoor trigger
• attacker chooses .
  • should differ from on the backdoor
  • but in general be -close to
• Defender is given either for randomly chosen or and is supposed to tell us which one it got.

main results

• statistical defndability iff .

• comp defendability

  • decisions trees are defendable
  • but not all of P

• In some sense requiring to be chosen randomly is a little bit unfortunate.

• But, you can’t just let it be chosen arbitrarily…

background

• HLW one inclusion graph thing is important for this.
• I mean, maybe you just need it as a black box, but it seems like a nice result.

sec4 stat defend

prediction strategy:

• There is a function which you don’t have access to(!)
• But, you get some samples from
• Your task is to guess the output of on some new point, after being given the value of on some random points.

This might seem totally hopeless. But! We’re assuming that comes from a class of functions with bounded VC dimension.

For instance, imagine that was the indicator function for a line. Then, after giving you a couple examples of things on and not on the line, you can totally figure out whether a new point is on the line or not.

So why is this good for us? We’ll do the following thing:

• Sample some ‘s and compute some ‘s where is the function that we’re given — which is either or .
• Then, we’ll try to use the HLW prediction strategy to figure out with good pr.
• This will work great if we started with .
• It will also work great if on all of the points that we queried.
• It won’t work if on any of our query points.
• But, we’re going to assume that that’s unlikely.
• i.e., that is only “imperceptibly” different from . By which I mean the difference is at most .
• So each of these strategies should work with good pr.
• So we can take a majority vote and win.

thm
If then you’re toast — backdoor is statistically indistinguishable from non-backdoor.
If then you’re good — backdoor is detectable with
pf of theorem

You’re screwed for large — then the adv can basically make the backdoor insertion correspond to switching between two legit functions. (remember that the adv doesn’t get to choose the backdoor location, but they do get to choose input distribution)

You win for small — we just run the strat outlined above. It works.

Intuition for proof: if small rel to then back-doored function is “very weird”.

sec5 computational

Strategy in prev section is not efficient (bc the HLW algorithm is not efficient).

Claim that PAC learnable things are efficiently defendable:

Proof

• you just do the pf from sec4 but you use the fact that PAC learnable things are learnable — you replace the HLW thing with this nice observation

Theorem in random oracle model, there are some things which are efficiently defendable but not efficiently PAC learnable

Proof Define to be the set of bit strings — we call these “keys”. Let also be the set of bit strings. This is the domain of our functions. Like we have functions . Define . Claim 1 this thing is efficiently defendable. proof: These functions are super far apart — all are at distance about . So, there are no valid nearby .

Claim 2 this thing is not efficiently PAC learnable.

Proof: it’s just random lol.

the story on whitebox or not

• For defendability they always assume whitebox access.
• When talking about PAC learning, they always mean that you ONLY get SAMPLES.
• In particular, for purposes of learning, you don’t get queries and definitely don’t get whitebox access to the thing.
• So basically their “this is defendable but not PAC learnable” claims are saying “we’re doing something interesting with either the whitebox access, blackbox query access, or the fact that we don’t need to output the function just tell if it’s weird or not.”
• Learning a function doesn’t make any sense if you have whitebox access to the function
• you could define learning with blackbox access, but they don’t

Conjecture Assuming OWF, there is a polynomially evaluatable rep class that is effic defendable but not effic PAC learnable. in other words, we’re going to try to replace the random oracle assumption with assumption that PRF’s exist.

Proof Maybe assuming CRHF’s is helpful. Minimum distance PRFs — sounds interesting.

sec 5.3 Assuming iO, there are polynomial sized circuits that aren’t defendable

punctured PRFs

You start with a function Then you choose some set . Then you can make a punctured key such that for all

BUT to a probabilistic polynomial time algorithm that knows BUT NOT , for any , the values still look pseudorandom.

remark: standard PRF construction can apparently be modified a tiny bit to become puncturable.

Proof that there are functions in P which aren't defendable

Let be a puncturable PRF

Then the argument is as follows:

1. indisting
2. compute the same function so by iO are indisintuishable
3. indistinguishable from or else violates puncturabililty.

sec 6 defending a tree

This seems like a nice theoretical result that also gives a lot of intuition for why mechanistic anomaly detection should be possible. Anyways I’m excited to read about this.

Actually I’m going to put this at the top of the post, because I think it’s that cool.

sec 7 implications and future work

Nevertheless, we still do not have an example of a natural representation class that is efficiently defendable but not efficiently PAC learnable. We consider finding such an example to be a central challenge for follow-up research. One possible candidate of independent interest is the representation class of shallow (i.e., logarithmic-depth) polynomial size Boolean circuits, or equivalently, polynomial size Boolean formulas. Question 7.1. Under reasonable computational hardness assumptions, is the representation class of polynomial size, logarithmic-depth Boolean circuits over {0, 1}n efficiently defendable? This representation class is known to not be efficiently PAC learnable under the assumption of

I think they’re basically just saying they want some “more natural” examples of things which are easy to defend but hard to learn.

Another question they pose is:

What if instead of requiring the backdoor to be randomly inserted you had a computationally bounded adversary that got to choose where to put the backdoor?

todo: add fancy new results that I prove here :)

I’m hoping to ultimately build up to some interesting classes of circuits (e.g., log-depth circuits). But, as I like to say “you should start somewhere tractable”. So we’re going to start with some silly classes of circuits. In what follows, the input space will always be and we consider the uniform distribution on this set.

Proposition Let be the class of depth circuits that just use a single gate, and they can inputs if they want. This function class is -defendable with confidence very efficiently.

Proof\

claim 1: If is too short, (an AND of fewer than literals) then there are no functions that are -close to .
pf: clear.

So this means that the adversary better choose a formula that takes into account quite a few literals. But then is quite unlikely on a random input. So, probably we’ll have . And then that’ll be our 1-query algorithm.

Q

Does the one-bit case extend naturally to a multiple bit case? I’m willing to believe this, but would love to see it spelled out.

N q

Statistically solve the uniform case.

A general takeaway from this example: Adversary shouldn’t make too sparse and also shouldn’t make too sparse. Like I think we can maybe basically assume .

The intuition that drives all of this is “morally the only way to insert a backdoor is to put a little if statement that says if input is backdoor trigger, bx weird.” which is totally detectable with whitebox access to the function, provided the trigger.

Next up, constant depth circuits (i.e., AC0)

Remark: I know that AC0 is PAC learnable. But, maybe thinking of defense strategies for it (without appealing to learning) would still be instructive.

Some thoughts on solving low depth circuits

• Feels like maybe there’s some kind of regularization technique that we can use to discover a backdoor?
• Maybe the network should be robust to dropout?
• Wait no, that doesn’t make sense. These networks are supposed to not be learnable — that’s one of the main points!

colorings

Hard defection is rare implies defendable

Suppose that for all , for at least of , there are NO such that hard defects on from . Then, is defendable.

Proof: Just blacklist any input where (1) you defect, (2) you have a neighbor that hard defects from you. This doesn’t blacklist too much, but it does blacklist enough.

Here’s what hard defects means: It basically just means that 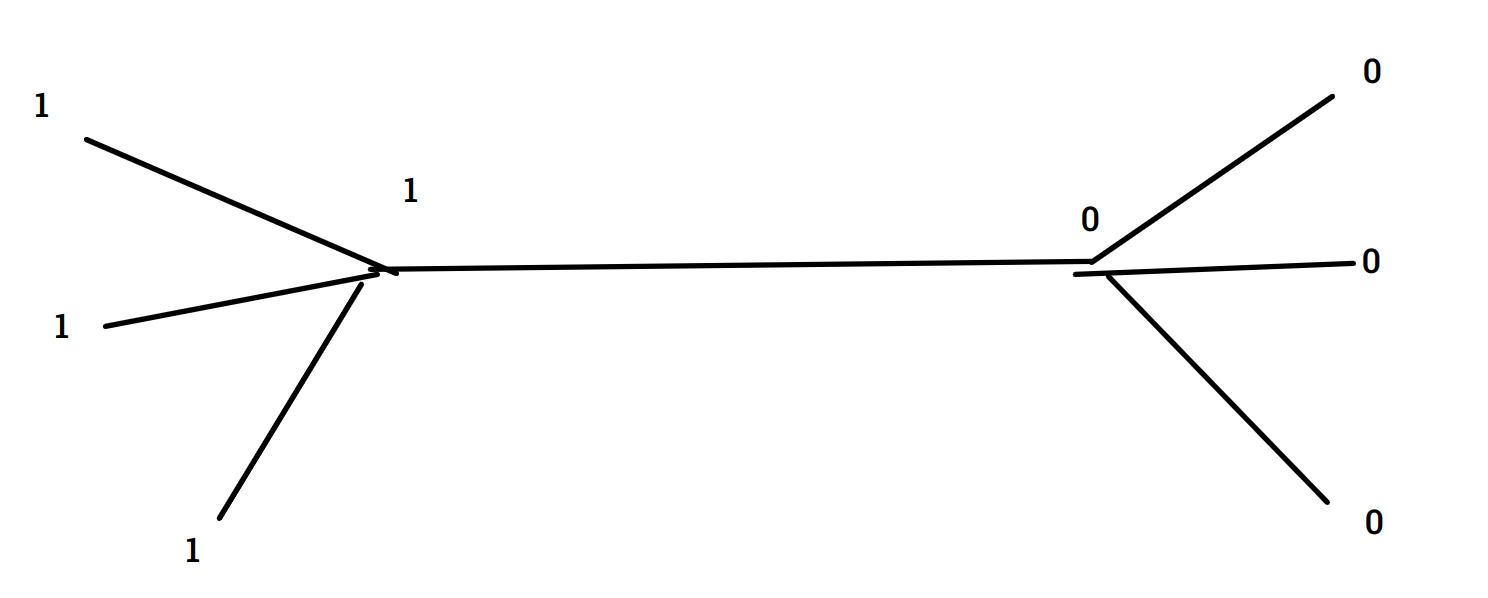has a strong majority for , while has a strong majority for . Maybe strong majority here means that a fraction of guys agree on the answer.

The reason I’m interested in the claim above, is because I think that the converse is almost kind of sort of true. Here’s what I have so far in terms of progress towards a converse:

Partial Converse to "Hard defection is rare implies defendable"

Suppose that for EVERY (yeah I don’t like this, but I’ll try to get rid of it in a minute) it is the case that for more than 20 percent of there is some so that hard defects from on . Then this is not defendable.

Wait actually I’m not totally sure this is true