some problems from my friends

A principle of interacting with people that is highly under-utilized is asking people for help. It’s possible to go too far with this, but I suspect you aren’t. The easiest way to employ this interacting with people strategy is, when interacting with someone you can think about the set of problems that you’re currently dealing with and talk about them with other people. A note of caution is that it’s bad to try to put responsibility for any decisions on other people — this is not responsible. But this is a service that most people are happy to provide and sometimes it’ll be useful. In my latest instantiation of trying this I asked some people for some cool math problems, because I wanted to get some exposure to some different topics. This saved me a lot of time trying to find good problems. Thanks!

Part 1 — Nathan — Complexity Theory

info theory basic facts

Let be an rv. Choose independent from . Shearer’s Inequality: .

This is saying, the average info you get from looking at a random subset of the coordinates of is at least the entropy of times the smallest probability of a coordinate being revealed.

This is obviously tight: suppose that the entropy of is all due to a single coordinate (all other coords are deterministic). Then this’d be tight.

Cross entropy: Joint entropy: . Mutual Info: .

crisp example of DKL asymmetry:

but .

if truth is then using as your code is super bad. not too terrible if is the truth and you use as your code.

NQ1: Prove that IP = PSPACE. note — I didn’t figure this one out — ended up just looking at wikipedia

The direction is simple I think — you can search over proofs. To prove the other direction probably we want to work with some complete problem like “determining the truth value of quantified 3CNF formulas”.

ok wikipedia suggested warming up by thinking about sharp-SAT. The Sharp-SAT problem is, given a formula and a number , check whether there are exactly sat assignments of the formula.

Here’s how we’re going to do it. Fix a formula . Let be an -bit prime (this is way overkill, we really only need bit prime; you can ask the prover to generate this for you iyw although no need) where is number of variables in the formula. Define to be an arithmetization of . Namely, we take , trade in for and trade in for . Define

The protocol is as follows:

1. Ask the Prover for the value of --- this is supposedly the number of SAT assignment of , if the Prover is being honest. The Prover hands over some number which may or may not actually be . (PS: the prime doesn’t mean derivative)
2. Ask the Prover to give you coefficients for the degree polynomial ; the Prover hands over some polynomial which may or may not be . 2. Check that . 3. This ensures that if is a lie, then .
3. Now, the verifier chooses a random and tells the prover about it.
   1. Because is a low degree polynomial, the chance that is pretty low. In particular low enough that we can union bound over all steps of the proof and assume that it never happens.
4. Anyways we kind of just continue on like this.
   1. The prover sends us .
   2. We check for consistency with .
   3. If was a lie, so if .
5. Finally at the end the prover will tell us some value and we can literally just check whether it’s true or not.

TQBF is in PSPACE.

We’re going to do something pretty similar, with a minor twist. Let’s arithmetize the formula again. We’re going to define pretty similarly to last time. That is, we’d like for any boolean inputs for it to be the case that

In order to get this what we can do is define

if the quantifier in question was a guy, and do an OR thing if it was an OR.

This is great but it doesn’t quite work because the degree blows up too much.

Luckily there is a way to reduce the degree. After every quantifier we intersperse these things which are like replace

not just for but for like everyone. Anyways this is kind of fine because it’s only polynomial overhead, and it ensures that the degrees never get too crazy.

nice.

NQ0: Prove the time hierarchy theorem + prove halting problem is undecidable. pf: Diagonalization

NQ2 Claim: .

Proof: Standard padding argument + Time hierarchy theorem.

Assume the claim is false, i.e., . Take --- exists by a diagonalization argument. Create which runs on the first bits of its input. Then , so by assumption there is an algorithm for . If on bit input has a certificate of length , then on an bit input has a proof of length --- just by padding its input. In other words, . But then by assumption has an algorithm running in time , contradiction.

NQ3 Claim 1: Show that every function has a circuit with gates. Proof Note: The below proof just uses gates of constant fan-in!

There’s a pretty simple way to make a circuit with gates for any function on bits --- basically you just do a tree where you split times and have one leaf corresponding to every possible variable assignment. But we’d like to do a bit better than this. So we’ll use the polynomial method (cite: RW). The number of boolean functions on bits is . Using the simple above method we can write down a circuit for every function on bits using gates. Now we can do the tree thing again, but stop when we reach the final bits. For these bits we can then just wire in one of the circuits that does the right thing. The total number of gates that we use in this scheme is

NQ3 Claim 2: Most functions need at least gates. Proof Number of functions you can make with gates is probably at most . Hence in order to make functions, it seems like we need to make .

NQ4 recall that in an arthur-merlin protocol, arthur first chooses some random bits to send to merlin, then merlin responds with a proof, which arthur verifies through some probablistic polynomial time algorithm. a language is in AM if there’s such a protocol with two-sided error 1%. you could also, for any k, define to be the k-round version of this, where arthur sends some random bits to merlin, merlin responds with the first part of the proof, arthur sends more random bits, etc. show that = AM for any constant k.

Proof For convenience I’m going to work with a complexity class which I call instead. Specifically in Arthur is a deterministic function of . Then we have:

I’d like to show that . To show this, it suffices to show that . Just for maximum clarity here’s what I’m talking about.

Procedure 1:

Arthur sends randomness r1
Merlin responds with proof pi1
Arthur runs a (deterministic) procedure on r1,pi1 and outputs accept / reject.  

Procedure 2: 
Arthur sends randomness r1
Merlin responds with proof pi1
Arthur sends randomness r2
Merlin responds with proof pi2
Arthur runs a deterministic procedure on r1,r2,pi1,pi2 and outputs accept / reject.  

Okay, how do we do it?!

Arthur’s procedure is as follows:

Let n^c be the maximum allowed length of pi1 in the two round protocol.  I can assume that this is polynomial because otherwise Arthur can't even recieve pi1! 
I guess you could think of some model where Arthur just gets random access to pi1? But I think we're not doing that. 

Anyways, send Merlin r1, r21,r22,r23...,r2,n^c (all at once)
And request merlin to produce pi1, pi21,pi22,...,pi2n^c
such that in the 2 round procedure we would've accepted this stuff

Arthur then runs the 2 round protocol on pi1,pi2k,r1,rik for each value of k. 
Arthur accepts if more than half of the 2 round protocol things accept, and rejects else.

Observation 1

For a statement in the language, say that is misleading if there aren’t any such that it’s 90% likely over choice of that there’s a proof such that Arthur accepts .

For a statement outside of the language, say that is misleading if there is some such that there’s more than a chance over choice of that there exists so that Arthur accepts .

Theorem: the chance that is misleading is at most .

Proof: Otherwise it’d violate our two-sided error bounds.

Lemma 2

Fix which isn’t misleading for statement X, and fix some . If you generate many ‘s and ask for ‘s with respect to all of them, then if X is true with probability we’ll have at least of the pairs are accepted by Arthur (if Merlin’s on the ball) and if X is false then with probability we’ll have at most of the proofs accepted by Arthur, no matter how hard Merlin tries.

Proof: Chernoff bouund

Now we union bound over all proofs . What we get at the end is, with probability 90%, the r1 is not misleading, in which case we have exponentially good probability that the fraction of proofs arthur accepts will be on the right side of . Namely, if Merlin is honest and the statement is true then Arthur will accept more than half of the proofs, and if the statement is false then even if Merlin is “crooked” Arthur won’t be tricked more than half the time.

In conclusion this means that we have a procedure that is great and it has 2-sided error but we can repeat it (in parallel) 100 times to get this back down to .

Note that the blow-up in proof complexity is like, if the proof complexity before was like then now we’re something like . Anyways, if you just do this once or twice it’ll be fine.

But we haven’t ruled out the possibility that is much much stronger than . I think is btw.

NQ5 You could define a k-round interactive proof to use private randomness. That is, consists of languages with a protocol similar to an Arthur Merlin protocol, but where instead of Arthur just sending all his random bits, he’s allowed to compute some arbitrary function of his random coins and send Merlin only that function. show that for any constant .

Part 2 — Alexis — information theory

Q1 Fix directed graph . We say that is a triangle if they form a directed 3-cycle . We say that is a wedge if we have the edges . Theorem: num triangles less or equal to num wedges.

Proof Let be uniformly random triangle. Then, . This is because the following both things correspond to the amount of additional surprise when you get if you choose a random cycle, and after already having revealed one of the vertices in the cycle, reveal the vertex following that one in the cycle. Therefore,

Let be a uniformly random wedge. We claim that:

To show this we’ll demonstrate a distribution on with entropy . The conclusion follows because the uniform distribution on a set is the maximum entropy distribution. To prove the inequality, here’s a distribution on wedges:

1. Sample and to be uniformly random wedges, but they are correlated (we condition on their first vertex being the same).
2. Output . This has the required edges .
3. And it has the required entropy.

Q2 Let iid and let iid. Let be the sorted version of . Def similarly.

Then

This is because is the same for all permutations of ‘s.

Finally,

by writing down the formula for divergence or thinking of divergence as suprise.

Here’s a cute application of this fact:

Q2.b Find .

Observe that is basically the same thing as So we have

by the problem about sorting. Neat.

Q3 For some reason I had trouble finding a nice definition of mutual information so I’m putting it here for all future people so that you can find it easily. It’s quite intuitive, it’s just the shared randomness amongst all three rvs. 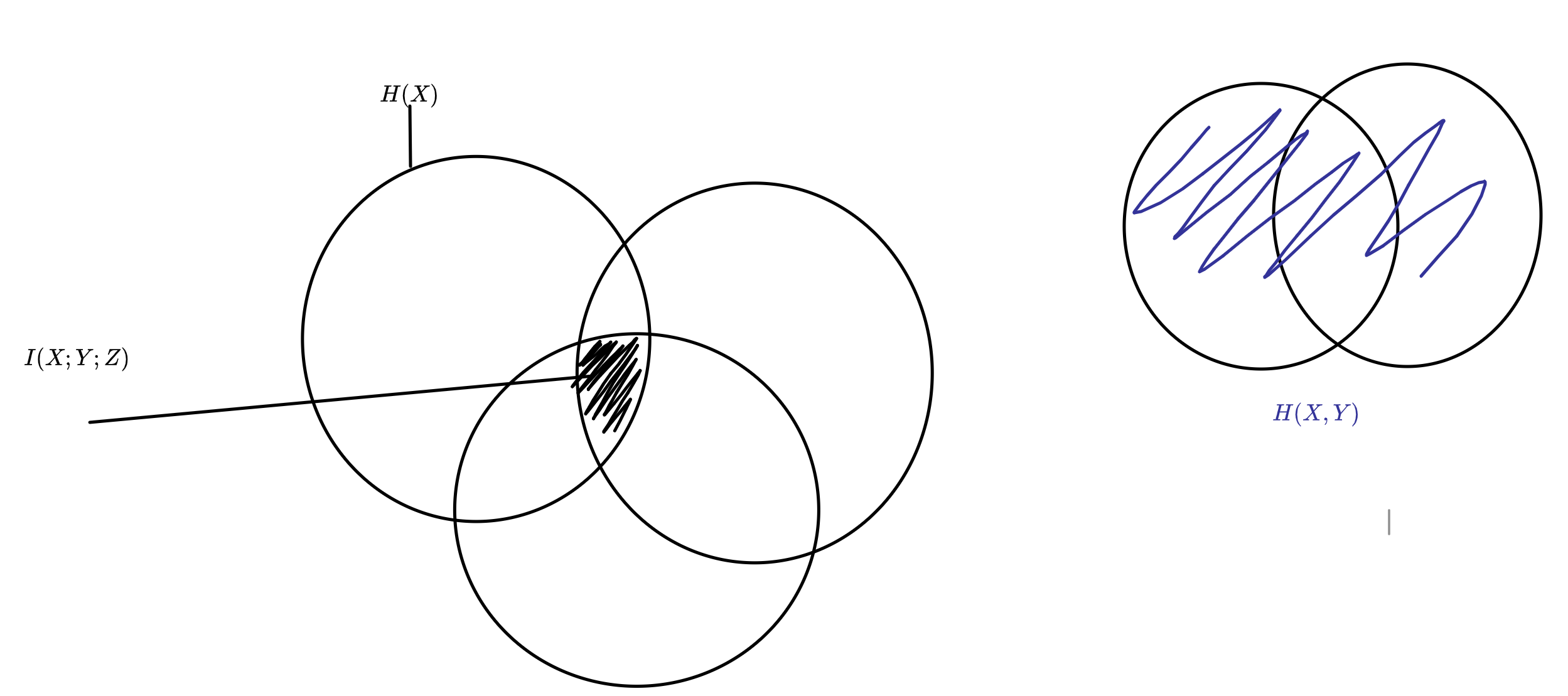Anyways, on to the question.

Q3a Suppose . Show that if and then .

(Note the difference between commas and semi-colons.)

For this problem I thought it’d be helpful maybe to know what the entropy in a Gaussian is. You can do some integral to find it — I just googled it.

where is the dimension. Morally speaking, it’s just the determinant of the covariance matrix plus some constant term depending on dimension.

---

ok that didn’t directly help me I guess. anyways, I had a long detour about normal random variables. Apparently if are jointly normal, meaning that they are of the form for some matrix and independent normal rvs , then if it follows that . I had a really hard time believing this because of the following example:

Where are indep standard normals. It seems pretty counter-intuitive to me that are independent. But if you write down their joint distribution it factors so what are you going to do.

Another thing I realized is that it’s hard to sqrt the covariance matrix. not literally hard, I think there’s a nice algo for it. but just hard for me.

---

Here’s another way of thinking about it. means that are independent and are independent. This implies that the covariance matrix between is diagonal, and similarly for the covariance matrix between .

---

Anyways I kind of give up on this problem for now.

Q3b The most classic question ever — give example of where but . My example is just where are independent random bits.

Q3c Give an example where but and also for all (we’re in discrete land). um ok My example is just where are independent random bits, where is . Fine.

---

some more information theory

Here’s an interesting question. I’ve done the computation but don’t get what it means yet.

Suppose you have a noisy channel. Specifically it works like this:

• always.
• goes to a random output.

Q: What is the capacity of this channel. I.e., how much information can you send in this channel?

It turns out that the right input distribution is as follows:

. This makes , the channel output, be . This distribution achieves .

A curious fact about this choice of : This choice of results in

Question: explain why this needs to be the case. Like:

1. Why does the best balance these expressions
2. Why is the mutual info captured by this KL divergence?

okay actually there’s a pretty simple explanation for all of this: First of all,

(you can see this identity by just writing out the definition of KL divergence). Anyways, this implies, by splitting up a sum,

So at this point we at least understand why, if the -divergences were balanced, then the MI would be equal to each of the KL divergences.

I still don’t have a great understanding of why we’d want the surprises to be the same…

---

digression TV distance:

---